特徵識別
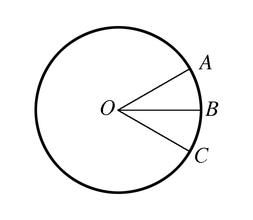
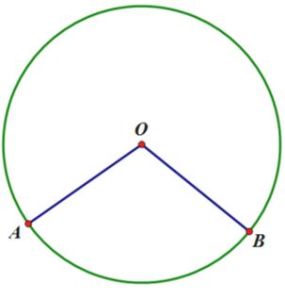 圓心角
圓心角②兩條邊都與圓周相交。
計算公式
①L(弧長)=n/180Xπr(n為圓心角度數,以下同);②S(扇形面積) = n/360Xπr²;
③扇形圓心角n=(180L)/(πr)(度)。
④K=2Rsin(n/2) K=弦長;n=弦所對的圓心角,以度計。
相關定理
圓心角定理
圓心角的度數等於它所對的弧的度數。圓心角、弧、弦、弦心距之間的關係
在同圓或等圓中,若兩個圓心角、兩條弧、兩條弦、兩條弦的弦心距中有一組量相等,則對應的其餘各組量也相等。理解:
(1)把頂點在圓心的周角等分成360份時,每一份的圓心角是1°的角。
(2)因為在同圓中相等的圓心角所對的弧相等,所以整個圓也被等分成360份,這時,把每一份這樣得到的弧叫做1°的弧。
(3)圓心角的度數和它們對的弧的度數相等.
推論:
在同圓或等圓中,如果(1)兩個圓心角,(2)兩條弧,(3)兩條弦(4)兩條弦上的弦心距中,有一組量相等,那么它們所對應的其餘各組量都分別相等。
圓心角與圓周角關係定理
在同圓或等圓中,同弧或同弦所對的 圓周角等於二分之一的圓心角。定理證明:分三種情況討論,始終做直徑COD,利用等腰三角形等腰底角相等,外角等於兩內角之和來證明。