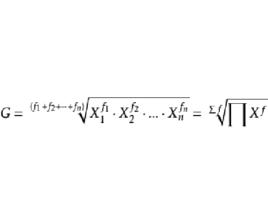基本介紹
幾何平均數
幾何平均數也稱 幾何均值，它是n個變數值連乘積的n次方根，是計算平均比率或平均發展速度最為適合的一種方法。凡是各變數值的連乘積等於總速度或總比率的現象都可以運用幾何平均法計算平均數。幾何平均數分為 簡單幾何平均數和 加權幾何平均數 。
加權幾何平均數定義
在計算幾何平均數時，某些變數值重複出現若干次，就出現了 加權幾何平均數公式，其計算公式為：
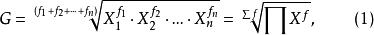加權幾何平均數
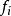加權幾何平均數
加權幾何平均數式中，為變數值重複出現的次數，又稱 權數。
簡單幾何平均數定義
簡單幾何平均數是n個變數值連乘積的n次方根，其計算公式為:
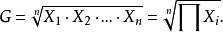加權幾何平均數 加權幾何平均數
加權幾何平均數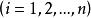
加權幾何平均數式中：——數列中第個變數值；
加權幾何平均數——變數值個數；
加權幾何平均數一連乘符號 。
相關結論
加權幾何平均數
加權幾何平均數
加權幾何平均數算術平均數、調和平均數和幾何平均數三者之間存在如下數量關係：
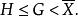加權幾何平均數並且只有當所有變數值都相等時，這三種平均數才相等，因此選擇平均數的計算公式十分重要。算術平均數公式的使用最為廣泛。
計算幾何平均數，一般需要開高次方：第一種方法是利用對數求解；第二種方法是利用計算器直接開高次方求解。
幾何平均數是適用於特殊數據的一種平均數；其套用條件有：（1）所掌握的變數值本身是比率的形式；（2）各比率的乘積等於總比率。幾何平均法一般適用於各變數值之間存在環比關係的事物。如銀行平均利率、各年平均發展速度、產品平均合格率等的計算。套用幾何平均數應注意的問題：（1）數列中任何一個變數值都不能為0，若有一個變數值等於0或負值，就無法計算幾何平均數；（2）幾何平均數易受最初水平和最末水平的影響。幾何平均數主要用於計算比率或速度的平均，因此，幾何平均數也可以看做是均值的一種變形。
例題分析
加權幾何平均數
例1 一家投資公司某筆投資的年利率是按複利計算的，10年的年利率分配是：第1年至第2年為5%；第3年至第5年為8%；第6年至第8年為10%；第9年至第10年為12%。求平均年利率。
解：由於以複利計算，各年的利息是在前一年累計存款額(本金加利息)的基礎上計息，因此應該先將各年利率換算成各年本利率(1+年利率),然後按加權幾何平均數計算平均年本利率，最後將平均年本利率減去1，就得到平均年利率。
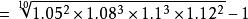加權幾何平均數平均年利率=平均本利率－1
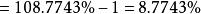加權幾何平均數結果說明，10年的平均本利率為108.774 3%，平均年利率即為8.774 3% 。
簡單幾何平均數
例2生產某產品需連續經過4 道工序，根據檢驗，各道工序的合格率分別為98%、95%、92%、90%，求該產品4道工序的平均合格率。
解:由於後道工序的產品合格率是在前道工序產品全部合格的基礎上計算而成的，因此整條裝配線的產品合格率不是各道工序產品合格率之和，而是各道工序產品合格率的連乘積。所以，不能採用算術平均數計算平均各道工序的產品合格率，而必須採用幾何平均數計算。即
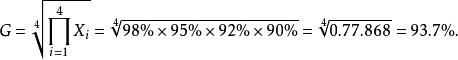加權幾何平均數以上兩例是幾何平均數兩種典型的套用場合 。
