歷史背景
統計指數從18世紀中葉物價指數產生開始，迄今已有三百多年的歷史了。
隨著歷史的推移，統計指數的套用不斷推廣到經濟領域的各個方面，因而統計指數的概念也不斷擴大和完善。當今在我國統計界一般認為：統計指數是研究社會經濟現象數量方面時間變動狀況和空間對比關係的分析方法。
統計指數書籍分類
同時還認為，統計指數有廣義和狹義之別。從廣義來說，凡是用來反映所研究社會經濟現象時間變動和空間對比狀況的相對數，如動態相對數、比較相對數和計畫完成情況相對數，都可稱為指數。
但從狹義來說，統計指數則是用來綜合反映所研究社會經濟現象複雜總體數量時間變動和空間對比狀況的一種特種相對數。所謂複雜總體是指不同度量單位或性質各異的若干事物所組成的、數量不能直接加總或不可以直接加總的總體。
必須明確，統計指數法中的統計指數概念，是指狹義指數而言，不是指廣義指數。
性質
正確套用統計指數，還必須要深刻了解統計指數的性質，概括的講，統計指數有一下性質。
相對性——統計指數總體各變數在不同場合下對比形成的相對數，它可以度量一個變數在不同時間或不同空間的相對變化。
綜合性——綜合性說明指數是一種特殊的相對數，它是由一組變數或項目綜合對比形成的。沒有綜合性，指數就不能發展成為一種獨立的理論和方法。
平均性——統計指數是總體水平的一個代表性指數。平均性的涵義有二：一是指數進行比較的綜合數量是作為個別量的一個代表，這本身就具有平均性；二是兩個綜合量對比形成的指數反映了個別量的平均變動水平。
分類
1．個體指數和總指數
統計指數按所研究對象的範圍不同，可分為個體指數和總指數。個體指數反映某種社會經濟現象個別事物變動的情況。如反映某一種商品物價變動的情況。總指數則綜合反映某種事物包括若干個別事物總的變動情況，如反映若干商品總的物價變動情況。有時為了研究需要，在介於個體指數與總指數之間，還編制組指數(或類指數)。組指數的編制方法與總指數相同。
2．數量指標指數和質量指標指數
統計指數按所表示的特徵不同，可以分為數量指標指數和質量指標指數。數量指標指數反映現象總體的規模和水平的變動狀況，如產量指數，職工人數指數等。質量指標指數則反映現象總體內涵質量的變動，如商品物價指數，勞動生產率指數等。
3．動態指數和靜態指數
統計指數按其本來的涵義，都是指動態指數。但在實際運用過程中，涵義漸漸推廣到了靜態事物和空間對比，因而產生了靜態指數。所謂靜態指數是指在同一時間條件下不同單位，不同地區間同一事物數量進行對比所形成的指數；或同一單位，同一地區計畫指標與實際指標進行對比所形成的指數。
4．定基指數和環比指數。
統計指數按在指數數列中所採用的基期不同，可以分為定基指數和環比指數。定基指數指在數列中以某一固定時期的水平作對比基準的指數；環比指數則是以其前一時期的水平作為對比基準的指數[1]。
作用
統計指數在社會經濟領域內廣泛套用，這是由於統計指數具有獨特的功能，能夠發揮重要的作用。具體表現在以下幾個方面：
(1)綜合反映複雜社會經濟總體在時間和空間方面的變動方向和變動程度。這是統計指數的最重要的作用。在社會經濟現象中，大量存在著不能直接加總或不能直接對比的複雜總體，為了反映和研究它們的變動方向和變動程度，只能通過統計指數法，編制統計指數才能得到解決。
(2)分析和測定社會經濟現象總體變動受各因素變動的影響。社會經濟現象總體中包含著數量因素和質量因素，通過編制數量因素指數和質量因素指數，可以分析和測定各因素變動對總體變動的影響。
(3)研究平均指標指數變動及其受水平因素和結構因素變動的影響。平均指標中包含水平因素和結構因素，因此可以編制可變組成指數，不變組成指數和結構影響指數，研究平均指標的變動及其各因素變動對平均指標變動的影響。
解釋
種類
可從不同的角度劃分：①按說明對象的範圍，可分為個體指數和總（組）指數；②按指標的性質，可分為數量指數和質量指數；③按基期是否固定，可分為定基指數和環比指數；④按資料範圍，可分為全面資料指數和代表選樣指數；⑤按計算方法，可分為綜合指數和平均數指數，其中平均數指數又可分為算術平均數指數、調和平均數指數和幾何平均數指數。
綜合指數
計算總指數的一種形式，是由包括兩個以上因素的總量指標對比而形成的指數。它將其中一個或一個以上的因素指標固定下來，觀察另一因素指標的綜合變動。固定下來的因素稱同度量因素，它使另一因素變得可以相加，同時也起著權數作用。以產品產量指數為例，其以基期生產價格作同度量因素的綜合指數噖公式為：
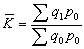
屬於質量指標這一類的商品物價指數，其綜合指數公式則可採用不同時期的同度量因素。它可得到不同的結果，具有不同的經濟內容。
①按基期銷售量作同度量因素計算：
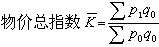
②按報告期銷售量作同度量因素計算：
用綜合公式編制總指數要求使用比較全面的資料，多在總體範圍比較小、現象比較簡單時套用。
平均數指數
計算總指數的又一形式。它是個體指數的平均數（加權或不加權）。常用的有加權算術平均數指數、加權調和平均數指數和簡單幾何平均數指數。①加權算術平均數指數。以產品產量指數為例，其算式為：
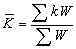
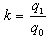為產量個體指數；W為權數。在有全面資料時，加權算術平均數指數實即綜合指數公式的變形
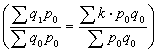，其權數要求為全面的基期生產額。但通常是只有非全面資料作權數，特別是在個體指數使用選樣資料時，計算加權算術平均數指數更具有獨立的意義。 ②加權調和平均數指數。以商品物價指數為例，其算式為：
為物價個體指數；M 為權數。在有全面資料時，加權調和平均數指數實即綜合指數公式的變形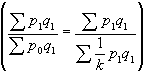
，其權數要求為全面的報告期實際銷售額。但通常是利用非全面資料作權數來獨立地計算調和平均數指數。 ③簡單幾何平均數指數。n個個體指數之積開n次方。與發展速度的幾何平均數意義相同（見平均數）。它不存在同度量因素的問題。以商品物價指數為例，其算式為：
簡單幾何平均數指數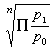
指數法的因素分析
複雜社會經濟現象總體中的各因素是互相聯繫的。指標上的聯繫也反映到指數中，形成指數體系，可用以對總體的變動作因素分析，如分析糧食產量變動中平均畝產與播種面積兩因素變動的影響。設A0、A1分別代表基期和報告期平均畝產,Q0、Q1分別代表基期和報告期播種面積，可得指數體系：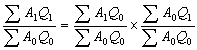
指數分子與分母的差：
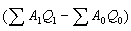
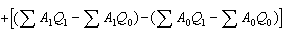
上述指數體系中，如只有一項未知，則利用其他已知項可以推斷。
統計指數還可用於平均指標動態的結構分析。因平均指標也是有被平均指標的各組水平和各組單位數比重兩個因素的複雜現象，固定一個因素指標就可反映另一因素指標的變動。
統計指數也可用於計畫檢查。套用的基本特點是用計畫指標和實際指標代替總指數中的基期指標和報告期指標。
此外,統計指數還可用於靜態的地區差異分析,如編制各地區的差價指數。以p0代表標準地區價格，p i（i=1,2,…）代表其他地區價格,則按簡單算術平均數指數計算的地區差價指數為：
