函式簡介
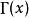 伽瑪函式
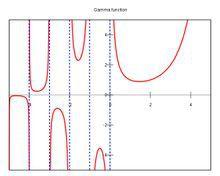
伽瑪函式伽瑪函式 (Gamma Function)作為階乘的延拓,是定義在複數範圍內的亞純函式,通常寫成 。
(1)在實數域上伽瑪函式定義為:
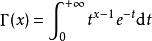 伽瑪函式
伽瑪函式(2)在複數域上伽瑪函式定義為:
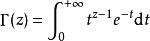 伽瑪函式
伽瑪函式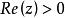 伽瑪函式
伽瑪函式其中 ,此定義可以用解析開拓原理拓展到整個複數域上,非正整數除外。
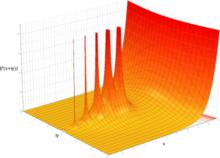 複平面上的Gamma 函式
複平面上的Gamma 函式(3)除了以上定義之外,伽馬函式公式還有另外一個寫法:
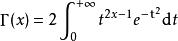 伽瑪函式
伽瑪函式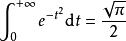 伽瑪函式
伽瑪函式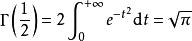 伽瑪函式
伽瑪函式我們都知道 是一個常用積分結果,公式(3)可以用 來驗證。
(4)伽馬函式還可以定義為無窮乘積:
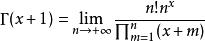 伽瑪函式
伽瑪函式不完全gamma函式
詳見不完全伽馬函式
歷史背景
1728年,哥德巴赫在考慮數列插值的問題,通俗的說就是把數列的通項公式定義從整數集合延拓到實數集合,例如數列1,4,9,16.....可以用通項公式n²自然的表達,即便 n 為實數的時候,這個通項公式也是良好定義的。直觀的說也就是可以找到一條平滑的曲線y=x²通過所有的整數點(n,n²),從而可以把定義在整數集上的公式延拓到實數集合。一天哥德巴赫開始處理階乘序列1,2,6,24,120,720,...,我們可以計算2!,3!,是否可以計算2.5!呢?我們把最初的一些(n,n!)的點畫在坐標軸上,確實可以看到,容易畫出一條通過這些點的平滑曲線。
 伽瑪函式
伽瑪函式 伽瑪函式
伽瑪函式但是哥德巴赫無法解決階乘往實數集上延拓的這個問題,於是寫信請教尼古拉斯·伯努利和他的弟弟丹尼爾·伯努利,由於歐拉當時和丹尼爾·伯努利在一塊,他也因此得知了這個問題。而歐拉於1729 年完美地解決了這個問題,由此導致了伽瑪 函式的誕生,當時歐拉只有22歲。
函式性質
1、通過分部積分的方法,可以推導出這個函式有如下的遞歸性質:
Γ(x+1)=xΓ(x)
於是很容易證明,伽馬函式可以當成是階乘在實數集上的延拓,對於正整數n,具有如下性質:
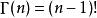 伽瑪函式
伽瑪函式2、與貝塔函式的關係:
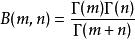 伽瑪函式
伽瑪函式3、在機率的研究中有一個重要的分布叫做 伽瑪分布:
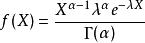 伽瑪函式
伽瑪函式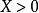 伽瑪函式
伽瑪函式其中 。
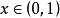 伽瑪函式
伽瑪函式4、對 ,有
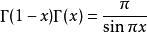 伽瑪函式
伽瑪函式這個公式稱為 余元公式。
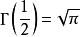 伽瑪函式
伽瑪函式由此可以推出以下重要的機率公式:
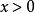 伽瑪函式
伽瑪函式5、對於 ,伽馬函式是嚴格凹函式。
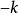 伽瑪函式
伽瑪函式6、伽馬函式是亞純函式,在複平面上,除了零和負整數點以外,它全部解析,而伽馬函式在 處的留數為
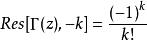 伽瑪函式
伽瑪函式Stirling公式
Gamma 函式從它誕生開始就被許多數學家進行研究,包括高斯、勒讓德、魏爾斯特拉斯、劉維爾等等。這個函式在現代數學分析中被深入研究,在機率論中也是無處不在,很多統計分布都和這個函式相關。Gamma 函式作為階乘的推廣,首先它也有和 Stirling 公式類似的一個結論:即當x取的數越大,Gamma 函式就越趨向於 Stirling 公式,所以當x足夠大時,可以用Stirling 公式來計算Gamma 函式值。
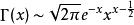 伽瑪函式
伽瑪函式函式內容
伽瑪函式的對數的導數稱為Digamma函式 ,記為
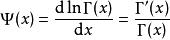 伽瑪函式
伽瑪函式。
Digamma函式同調和級數相關,其中
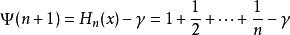 伽瑪函式
伽瑪函式其中
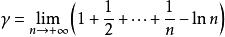 伽瑪函式
伽瑪函式是歐拉常數。
而對於任意x有
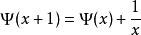 伽瑪函式
伽瑪函式在複數範圍內,Digamma函式可以寫成
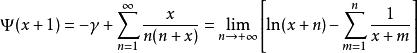 伽瑪函式
伽瑪函式而Digamma函式的泰勒展開式為
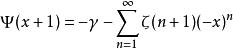 伽瑪函式
伽瑪函式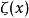 伽瑪函式
伽瑪函式其中函式 為黎曼zeta函式,是關於黎曼猜想的一個重要函式。
類似伽瑪函式,Digamma函式可以有漸進式:
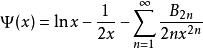 伽瑪函式
伽瑪函式積分形式
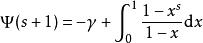 伽瑪函式
伽瑪函式digamma值
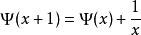 伽瑪函式
伽瑪函式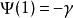 伽瑪函式
伽瑪函式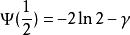 伽瑪函式
伽瑪函式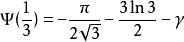 伽瑪函式
伽瑪函式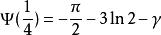 伽瑪函式
伽瑪函式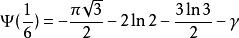 伽瑪函式
伽瑪函式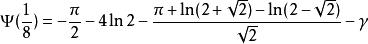 伽瑪函式
伽瑪函式函式套用
在Matlab中的套用
其表示N在N-1到0範圍內的整數階乘。
公式為:gamma(N)=(N-1)*(N-2)*...*2*1
例如:
gamma(6)=5*4*3*2*1
ans=120