定義
分母有理化,簡稱 有理化,指的是將該原為無理數的分母化為有理數的過程,也就是將分母中的根號化去。有理化後通常方便運算,有理化的過程可能會影響分子,但分子及分母的比例不變。
單項式
套用一般根號運算:
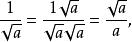 分母有理化
分母有理化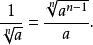 分母有理化
分母有理化二項式
套用平方差公式:
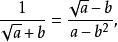 分母有理化
分母有理化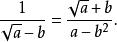 分母有理化
分母有理化套用立方和、立方差公式:
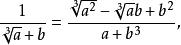 分母有理化
分母有理化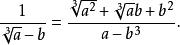 分母有理化
分母有理化多項式
逐項有理化
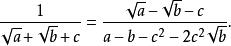 分母有理化
分母有理化輾轉相除法
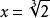 分母有理化
分母有理化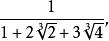 分母有理化
分母有理化設 有理化
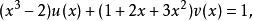 分母有理化
分母有理化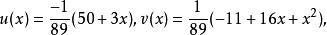 分母有理化
分母有理化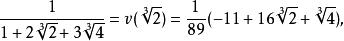 分母有理化
分母有理化待定係數法
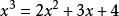 分母有理化
分母有理化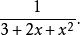 分母有理化
分母有理化,求
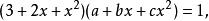 分母有理化
分母有理化設
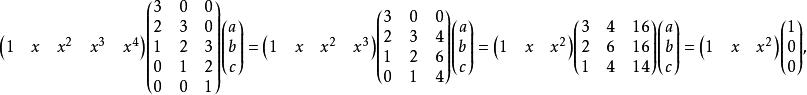 分母有理化
分母有理化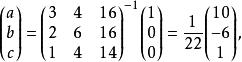 分母有理化
分母有理化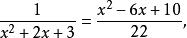 分母有理化
分母有理化常規方法
下面介紹兩種分母有理化的常規方法,基本思路是把分子和分母都乘以同一個適當的代數式,使分母不含根號 。
分母是一個單項式
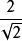 分母有理化
分母有理化例如二次根式 ,下面將之分母有理化:
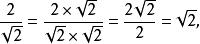 分母有理化
分母有理化分子分母同時乘以√2,分母變為2,分子變為2√2,約分後,分數值為√2。在這裡我們想辦法把√2化為有理數,只要變為它的平方即可。
分母是一個多項式
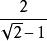 分母有理化
分母有理化再舉一個分母是多項式的例子,如 ,下面將之分母有理化:
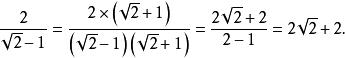 分母有理化
分母有理化思路仍然是將分子分母同乘相同數。這裡使用平方差公式,同時乘上√2+1,分子變為2√2+2,分數值為2√2+2,再約分即可。也就是說,為了有理化多項式的分母,原來分母是減號,我們乘上一個數字相同但用加號連線的式子,再用平方差公式。
此方法可套用到根式大小比較中去。
特殊方法
下面有一些特殊的方法供參考!
分解約簡法
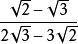 分母有理化
分母有理化將 分母有理化:
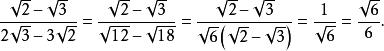 分母有理化
分母有理化這裡我們將分母分解因式後提取出來,這樣避免採用平方差公式分解。這種方法較適用於分子分母含有公因式時。
配方約簡法
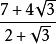 分母有理化
分母有理化將 分母有理化:
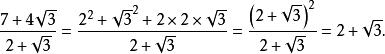 分母有理化
分母有理化這裡我們將分子化成平方式,然後利用完全平方公式配方,再和分母約分,這樣避免採用平方差公式分解 。
注意事項
下面舉一個含參數的二次根式:
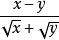 分母有理化
分母有理化將 分母有理化:
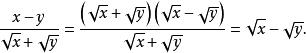 分母有理化
分母有理化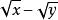 分母有理化
分母有理化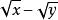 分母有理化
分母有理化在這裡我們將分子用平方差公式分解因式,然後分解!注意在這裡我們不能將分母乘以 ,因為 有可能等於0,若分情況討論又比較麻煩,此時我們就應該注意分子和分母的結構關係 !
拓展
有理化因式
例如:
將分子、分母同時乘以分母的有理化因式。
有理化因式舉例
如√a的有理化因式是正負√a,√a+√b的有理化因式是
√a-√b或√b-√a.

