對比區別
同類二次根式與同類項的異同
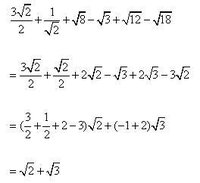同類二次根式同類二次根式與同類項無論在表現形式上還是運算法則上都有極類似之處，因此我們把二者的區別和聯繫列出，學習時注意辨析、對比來套用。
相同點
1. 兩者都是兩個代數式間的一種關係。同類項是兩個單項間的關係，字母及相同字母的指數都相同的項;同類二次根式是兩個二次根式間的關係，指化成最簡二次根式後被開方數相同的二次根式。
2. 兩者都能合併，而且合併法則相同。我們如果把啊最簡二次根式的根號部分看做是同類項的指數部分，把根號外的因式看做是同類項的係數部分，那么同類二次根式的合併法則與同類項的合併法則相同，即“同類二次根式(或同類項)相加減，根式(字母)不變，係數相加減”。
不同點
1. 判斷準則不同。
判斷兩個最簡二次根式是否為同類二次根式，其依據是“被開方數是否相同”，與根號外的因式無關;而同類項的判斷依據是“字母因式及其指數是否對應啊相同”，與係數無關。
2. 合併形式不同。
教學階梯
“同類二次根式定義”教學的三個梯級
“同類二次根式定義”教學的三個梯級為：
(1)實例引入同類二次根式定義，舉正反例反覆理解;
(2)定義套用，充分理解“化簡後，被開方數相同的二次根式”，並舉幾組不是最簡二次根式的例子進行理解;(3)定義的拓廣，從同類二次根式定義中發現一般同類根式的定義(新教材正文不做要求)。
拓展套用
二次根式是初二代數最重要的內容，同類二次根式又是其中最重要的概念之一。人教版國中《代數》第二冊第189面關於同類二次根式的描述是“幾個二次根式化成最簡二次根式以後，如果被開方數相同，這幾個二次根式就叫同類二次根式”，顯然此定義是建立在最簡二次根式基礎之上的。
由於題目未講明與是否是最簡二次根式，同學們普遍感到難以下手。求解時，大多數同學的做法是先假定兩根式都為最簡二次根式，然後由同類二次根式的定義列出等式解的。為了檢查正確與否，最後又進行了驗算，將代入原題，得到的根式是做為特例，它們滿足題意，是同類二次根式。於是題目得到了圓滿解決，選擇答案B。
恰在此時，個別愛動腦筋的同學發出了自己的疑問，驗算時，得到的與都不是最簡二次根式，這與我們解題時的假設互相矛盾!一時全班啞然。
為了調動同學們的積極性，我讓同學們相互間展開討論，同時自己也展開思考。經過共同努力發現問題出在同類二次根式的概念上，概念講明最終比較時是看最簡二次根式的被開方數。而在上題中，兩根式有意義的充要條件是在此範圍內兩根式的被開方數都是分數，根式根本不可能是最簡二次根式，所以我們作出了的假設原本就不成立，也就意味著此題不能直接用課本定義加以判斷，必須對同類二次根式的概念加以挖掘和拓展!
根據課本定義有以下兩點值得注意：不論幾個二次根式是否為最簡二次根式都有：1。若被開方數相同，必為同類二次根式，如與;2。經過一步或幾步變形，若被開方數相同，必為同類二次根式。如，可變形為即可判斷;或將變形為也馬上可以判斷;甚至可將變為，同時將變為作最終判斷。
有了以上兩點，問題已迎刃而解，原題不必作任何假設，直接將原式被開方數比較，或者將其一或二者經一步或數步變形後再比較被開方數，即可得到結論。象這樣未指明是否是最簡二次根式的情況都有無數組解。此題同樣有無數組解，答案C是滿足題意的一個解。
通過此題的探索，使我們得到了判斷同類二次根式的更簡單和更廣泛的方法，不必將原式化成最簡二次根式，也不必關心它們是否是最簡二次根式，只需直接觀察被開方數可否化成相同的值即可得到結論。
