定義性質和概念
如果一個數的平方等於a，那么這個數叫做a的平方根。a可以是具體的數，也可以是含有字母的代數式。
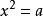二次根式即：若
，則x叫做a的平方根，記作x=
。其中a叫被開方數。其中正的平方根被稱為算術平方根。
關於二次根式概念，應注意：
被開方數可以是數 ，也可以是代數式。被開方數為正或0的，其平方根為實數；被開方數為負的，其平方根為虛數。
性質：
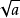二次根式1.任何一個正數的平方根有兩個，它們互為相反數。如正數a的算術平方根是
，則a的另一個平方根為﹣
；最簡形勢中被開方數不能有分母存在。
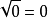二次根式2.零的平方根是零，即
；
3.有理化根式：如果兩個含有根式的代數式的積不再含有根式，那么這兩個代數式互為有理化根式,也稱互為有理化因式。
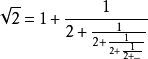二次根式4.無理數可用有理數形式表示, 如:
。
幾何意義
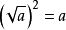二次根式1°
(a≥0)[任何一個非負數都可以寫成一個數的平方的形式；利用此性質在實數範圍內因式分解];
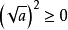二次根式2°
，
都是非負數；當a≥0時，
；而
中a取值範圍是a≥0，
中取值範圍是全體實數。
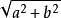二次根式3°c=
表示直角三角形內，斜邊等於兩直角邊的平方和的根號，即勾股定理推論;
4° 逆用可將根號外的非負因式移到括弧內，如
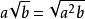二次根式
二次根式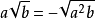﹙a>0﹚ ，
﹙a<0﹚
二次根式﹙a≥0﹚ ，
﹙a<0﹚
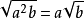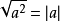二次根式7° 注意:
，即具有雙重非負性。
算術平方根
正數a的正的平方根和零的平方根統稱為算術平方根，用(a≥0)來表示。
0的算術平方根為0.
開平方運算
化簡
化簡二次根式是國中階段考試必考的內容，國中競賽的題目中也常常會考察這一內容。
最簡二次根式
二次根式化簡一般步驟：
①把帶分數或小數化成假分數；
②把開方數分解成質因數或分解因式；
③把根號內能開得盡方的因式或因數移到根號外；
④化去根號內的分母，或化去分母中的根號；
⑤約分。
運算法則
乘除法
1.積的算數平方根的性質
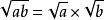二次根式（a≥0，b≥0）
2. 乘法法則
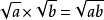二次根式（a≥0，b≥0）
二次根式的乘法運算法則，用語言敘述為：兩個因式的算術平方根的積，等於這兩個因式積的算術平方根。
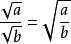二次根式3.除法法則
（a≥0，b>0）
二次根式的除法運算法則，用語言敘述為：兩個數的算術平方根的商，等於這兩個數商的算術平方根。
套用
二次根式的套用主要體現在兩個方面：
（1）利用從特殊到一般，再由一般到特殊的重要思想方法，解決一些規律探索性問題；
（2）利用二次根式解決長度、高度計算問題，根據已知量，求出一些長度或高度，或設計省料的方案，以及圖形的拼接、分割問題。這個過程需要用到二次根式的計算，其實就是化簡求值。
二次根式的性質和最簡二次根式
判斷一個二次根式是否為最簡二次根式主要方法是根據最簡二次根式的定義進行，或直觀地觀察被開方數的每一個因數（或因式）的指數都小於根指數2，且被開方數中不含有分母，被開方數是多項式時要先因式分解後再觀察。
例：√8、√18、√32、√2、3√3、5√5中哪些是最簡二次根式？
答：√2、3√3、5√5是最簡二次根式。
從上面的例子可以看出，遇到一個二次根式，將它化簡會給解決問題帶來方便．
滿足下列兩個條件的二次根式，叫做最簡二次根式：
(1)被開方數的因數是整數，因式是整式；
(2)被開方數中不含能開得盡方的因數或因式．
1）
a（a≥0）
√ā=|a|={
-a（a＜0）
√a/b=√a /√b（a≥0，b>0）
條件：
（1）被開方數的因數是整數或字母，因式是整式；
（2）被開方數中不含有可化為平方數或平方式的因數或因式。
如：不含有可化為平方數或平方式的因數或因式的有√2、√3、√a（a≥0）、√x+y 等；
含有可化為平方數或平方式的因數或因式的有√4、√9、√a^2、√（x+y）^2、√x^2+2xy+y^2等
二次根式的乘法和除法
√a·√b=√ab（a≥0，b≥0）
√a/b=√a /√b（a≥0，b>0）
二數二次根之積，等於二數之積的二次根。
如果兩個含有根式的代數式的積不再含有根式，那么這兩個代數式叫做共軛因式，也稱互為有理化根式。
開平方運算：
求一個非負數的平方根的運算，叫做開平方。開平方與平方互為逆運算。
化簡：
化簡二次根式是國中階段考試必考的內容，國中競賽的題目中也常常會考察這一內容。
最簡二次根式定義(❶被開方數不含分母❷被開方數中不含能開得盡的因數或因式)
二次根式化簡一般步驟：
①把帶分數或小數化成假分數
②把開方數分解成質因數或分解因式
③把根號內能開得盡方的因式或因數移到根號外
④化去根號內的分母，或化去分母中的根號
⑤約分
分母有理化：
在分母含有根號的式子中，把分母的根號化去，叫做分母有理化。
分母有理化即將分母從非有理數轉化為有理數的過程，以下列出分母有理化的幾種方法：
(1)直接利用二次根式的運算法則：
例：√a/√b=(√a*√b)/(√b*√b)=√ab/b(a≥0,b>0)
(2)利用平方差公式：
例：1/(√a+√b)=(√a-√b)/(√a-√b)(√a+√b)=(√a-√b)/(√a)^2-(√b)^2=(√a-√b)/(a-b)(a≥0,b≥0,a≠b)
(3)利用因式分解：
例：(1+2√a-√b-√ab)/(1+√a-√b)=(1+√a-√b)(1+√a)/(1+√a-√b)=1+√a(此題可運用待定係數法便於分子的分解)
(4)利用約分：(x-y)/(√x+√y)=(√x+√y)(√x-√y)/(√x+√y)=√x-√y(x>0,y>0)
分子有理化：
把分子中的根號化去，叫做分子有理化。
√a+√b=(√a+√b)(√a-√b)/(√a-√b)=a-b/(√a-√b)(a≥0,b≥0,a≠b)
換元法
換元法即把根式中的某一部分用另一個字母代替的方法，是化簡的重要方法之一。
例：在根式√[x+11-6√(x+2)]+√[x+27-10√(x+2)]中，令u=√(x+2)，即可得到
原式=√(u^2+9-6u)+√(u^2+25-10u)=√(u-3)^2+√(u-5)^2=2u-8=2√(x+2)-8
分析：通過換元法換元，將根號下的數化簡，最後求值。
【練習題】
選擇題：
1.若√(3-m)為二次根式，則m的取值為()
A.m≤3B.m<3C.m≥3D.m>3
2.對於二次根式√(x^2+9)，以下說法不正確的是()
A.它是一個正數B.是一個無理數
C.是最簡二次根式D.它的最小值是3
填空題：
3.當x___________時，√(1-3x)是二次根式.
4.比較大小：-3√2______-2√3.
簡答題
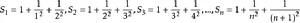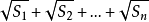二次根式
二次根式nn
6.化簡
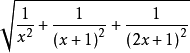二次根式.
7.已知
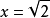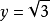二次根式，
二次根式，求
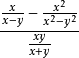二次根式的值
8.
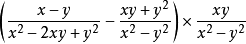二次根式，其中
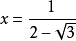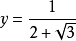二次根式，
二次根式9.
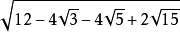二次根式10.
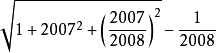二次根式11.已知x、y滿足
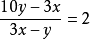二次根式，且
≠0，求
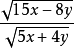二次根式的值
12.設
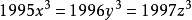二次根式，
>0且
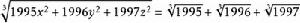二次根式，試求
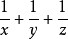二次根式的值
【參考答案】
選擇題：
1.A
2.B
填空題：
3.≤1/3
4.<
簡答題
5-12 略
運算
加減法
一般地，把幾個二次根式化為最簡二次根式後，如果它們的被開方數相同，就把這幾個二次根式叫做同類二次根式。
2、合併同類二次根式
把幾個同類二次根式合併為一個二次根式就叫做合併同類二次根式。
3、二次根式加減時，可以先將二次根式化為最簡二次根式，再將被開方數相同的進行合併。
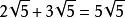二次根式例如：（1）
；（2）
乘除法
二次根式相乘除，把被開方數相乘除，根指數不變，再把結果化為最簡二次根式
乘法
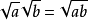二次根式﹙a≥0，b≥0﹚
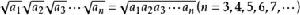二次根式推廣
﹙a≥0﹚
2.除法
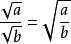二次根式﹙a≥0，b>0﹚
推廣
二次根式.
﹙a≥0，b>0﹚
混合運算
二次根式混合運算與實數運算相同的運算順序相同，先乘方，在乘除，後加減，有括弧的先算括弧裡面的。
乘法公式
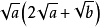二次根式❶
型，運用分配律化簡，原式
。
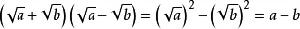二次根式❷
， ﹙a≥0，b≥0﹚直接運用平方差公式。
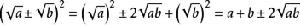二次根式❸
， ﹙a≥0，b≥0﹚直接運用完全平方公式。
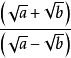二次根式❹
型
運算方法
1、確定運算順序。
2、靈活運用運算定律。
3、正確使用乘法公式。
4、大多數分母有理化要及時。
5、在有些簡便運算中也許可以約分，不要盲目有理化。
6、字母運算時注意隱含條件和末尾括弧的註明。
7、提公因式時可以考慮提帶根號的公因式。
共軛根式
共軛根式
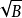二次根式當A,B,C,D都是有理式，而
,
中至少有一個是無理式時，稱
和
互為共軛根式。這兩式的積是有理式
兩個根式互為共軛根式，則他們互為有理化因式
共軛虛根(證明)
【共軛】:複數中，實部相等，而虛部互為相反數的一對複數，稱為共軛複數對
形如：a+bi 和a-bi
【求根公式】：
對於任意一個一元二次方程ax+bx+c=0,
它的兩個根是 ： [-b-√(b-4ac)]/2a,[-b+√(b-4ac)]/2a
這是由配方法求得的公式。
當b-4ac< 0 時，√(b-4ac) = √(4ac-b) i
所以，方程的兩個根就變為 ：
-b/2a-√(4ac-b)/2a i 和 -b/2a+√(4ac-b)/2ai
這樣，
兩根的實部都為 -b/2a
兩根的虛部 （-√(4ac-b)）/2a和 +（√(4ac-b) ）/2a互為相反數
兩根就成為了 共軛的一對復根了
zzˊ。
根據定義，若z=a+bi(a，b∈R)，則zˊ=a－bi（a,b∈R)。共軛複數所對應的點關於實軸對稱
1.代數特徵：
（1）|z|=|z′|；
（2）z+z′=2a（實數），z-z′=2bi；
（3）z·z′=|z|2=a+b（為一實數）；
（4）z″=z．
2.運算特徵：
（1）(z+z)′=z′+z′
（2） (z-z)′=z′-z′
（3） (z·z)′=z′·z′
（4） (z/z)′=z′/z′ (z≠0)
3 模的運算性質：
① |z·z| = |z|·|z|
②
③┃|z|－|z|┃≤|z+z|≤|z|+|z|
|z－z| = |z－z|，是複平面的兩點間距離公式，由此幾何意義可以推出複平面上的直線、圓、雙曲線、橢圓的方程以及拋物線
ps:z′表示複數z的共軛複數(實際形式為z上一橫)，z″表示複數z的共軛複數的共軛複數(為z上兩橫)
題目
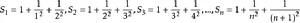二次根式① 設
. 求
的值(用含有n的代數式標識,其中n為正整數).
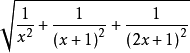二次根式化簡
.
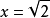二次根式②已知
，
，求
的值
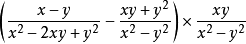二次根式③
，其中
，
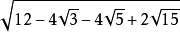二次根式④
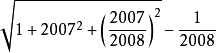二次根式⑤
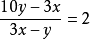二次根式⑥已知x、y滿足
，且x≠0，求
的值
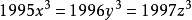二次根式⑦設
，xyz>0且
，試求
的值
分母有理化
分母有理化有兩種方法
I.
如:√a/√b=√a×√b/√b×√b=√ab/b
如圖
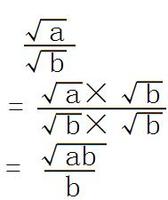二次根式一
II.
要利用平方差公式
如1/√a＋√b=√a－√b/(√a＋√b)(√a－√b)=√a－√b/a－b
如圖二
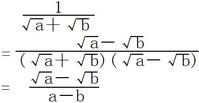二次根式