函式的連續性
正文
描述函式的一種連綿不斷變化的狀態，即自變數的微小變動只會引起函式值的微小變動的情況。確切說來，函式在某點連續是指：當自變數趨於該點時，函式值的極限與函式在該點所取的值一致。一元連續函式 設函式ƒ(x)在x＝α附近（包括x=α處）有定義。若
，
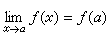如在(*)中，x →α改為x →α-0或x →α+0,即限定x<α或x>α,則稱ƒ(x)在x=α處左連續或右連續。顯然ƒ(x)在x=α處連續的必要充分條件為它在α處左、右都連續。
如
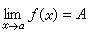存在，但A≠ƒ(α)或 ƒ(α)沒有意義，則稱ƒ(x)在α處為可去間斷（可去不連續）,因為這時只要改變或補充定義ƒ(α)使其等於A就可使它變得在α處連續；因此，這種不連續常常算作是連續的。如果x→α時，則稱ƒ(x)在α處有第一類間斷，B-A稱為其躍度。不屬於上述情況的不連續點都稱為第二類間斷。 如果ƒ(x)在一開區間(α，b)內每一點都連續,則稱ƒ(x)在開區間(α，b)內連續。ƒ(x)在一閉區間【α,b】上連續是指：在開區間(α,b)內連續,而在α處右連續和b處左連續。
由此可確切定義幾何名詞連續曲線。設平面曲線 C可寫成參數方程
x =x(t), y =y(t) (α≤t≤β)，
其中x(t)、y(t)都是【α,β】上的連續函式,則稱C是連續曲線。此定義顯然可推廣到空間曲線甚至一般的 n維空間中的曲線上去。連續函式的性質
① 如ƒ(x)、g(x)都在x=α處連續，則ƒ(x)±g(x)，ƒ(x)g(x)，
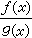（只要g(α)≠0)也在x=α處連續。 ② 如ƒ(x)在x=α處連續，且ƒ(α)≠0，則必在x＝α的某一小δ鄰域（即|x-α|<δ）中，ƒ(x)不變號,即ƒ(x)與ƒ(α)同號。
③ 在閉區間上的連續函式,必有上界和下界，且有最大值和最小值，並能取最小值和最大值之間的一切中間值。
還可證明，所有初等函式在其有定義的區間上都是連續的。
設I為一閉或開的區間，如果任給ε>0,必有δ>0存在，使對I中任何兩點x，x′，只要|x-x′|<δ，便有｜ƒ(x)-ƒ(x′)|<ε，則稱ƒ(x)在I上一致連續。關於一致連續性有下面的重要定理：在閉區間上的連續函式一定在該區間上一致連續。這一定理有時稱作康托爾定理。
多元連續函式 設
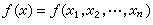為一 n元函式,這裡x=(x1,x2,…,xn)為n維向量或n維空間中一點，而α=( α1,α2,…,αn)為一定點。如果(1)式成立,亦即對任給ε>0，必有δ>0存在，使當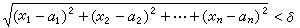 
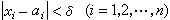
｜ƒ(x)-ƒ(α)｜<ε
,則稱ƒ(x)在α處連續。也可類似地定義ƒ(x)在n維區域G中連續和一致連續。不過，當α是ƒ(x)定義域G邊界上的一點時，在上面定義中要限制x在G及其邊界上。一元連續函式的上述性質都可推廣到多元函式上來，康托爾定理這時也成立,不過在其中區間I要換成有界閉區域。和連續曲線類似，也可定義連續曲面等等。
以上連續函式的定義也可推廣到復變數的複函數上來（見複變函數）。
連續函式的定義還可推廣到一般抽象的拓撲空間的情況。設X，Y是兩個拓撲空間,ƒ:X→Y是把X映入Y的一個映射,又α∈X,如果對於ƒ(α∈Y的任一鄰域
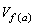，存在著α的一鄰域Uα，使 
，
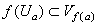