函式形式
含參變數α(α>0)的反常積分：
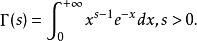Г函式性質
收斂性
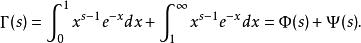Г函式Φ（s）的收斂性：當s≧1時是正常積分，所以其收斂；當0〈s〈1時，由柯西判別法可推得其是收斂的。
Ψ（s）的收斂性：當s〉0時，由柯西判別法推得其是收斂的。
故含參量積分Γ（x）在s〉0時收斂，其定義域為s〉0。
連續性
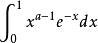Г函式
Г函式
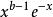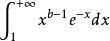Г函式
Г函式在任何閉區間[a,b]（a>0）上，對於函式Φ（s），當0〈x≦1時有 ≦ ，由於 收斂，從而Φ（s）在[a,b]上收斂；對於Ψ（s），當1≦x〈+∞時，有 ≦ ，由於 收斂，從而Ψ（s）在[a,b]上也一致收斂。於是Γ（s）在s〉0上連續。
可導性
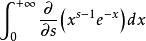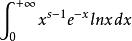Г函式
Г函式考察積分 = 。它在任何區間[a,b](a〉0)上一致收斂。於是由含參量反常積分的可微性得出Γ（s）在[a,b]上可導，由a，b的任意性，Γ（s）在s〉0上可導。
遞推公式
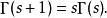Г函式證明：
對下述積分套用分布積分法，有
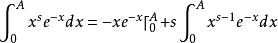Г函式
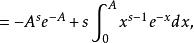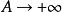Г函式
Г函式令 就得到Γ函式的遞推公式：
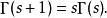Г函式推論：
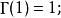Г函式
Г函式當s趨於0時， Γ（s）趨於+∞
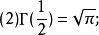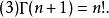Г函式
Г函式Γ函式的圖像
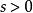Г函式
Г函式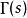
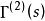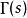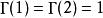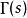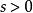Г函式 Г函式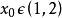
Г函式 Г函式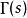 Г函式
Г函式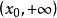
Г函式 Г函式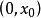
Г函式
Г函式對於一切 ， 和 恆大於0，因此 的圖像位於s軸的上方，且是向下凸的。因為 ，所以 在 上僅存在的極小值點 且 。又 在 內嚴格增，在 內嚴格減。
由於
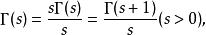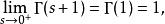Г函式
Г函式所以
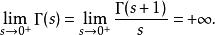Г函式
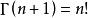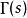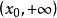Г函式 Г函式 Г函式由 和 在 上嚴格增可得：
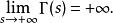Г函式
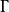Г函式
Г函式綜上所述， 函式的圖像如圖1中s>0部分所示 。
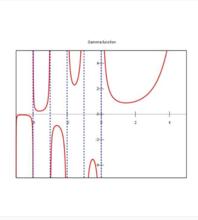圖1.伽馬函式Γ函式與Β函式之間的關係
對於任意的實數p，q：
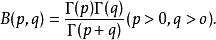Г函式套用
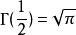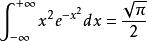Г函式
Г函式已知 ，試證 。
證明：
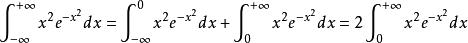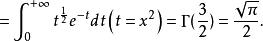Г函式
Г函式