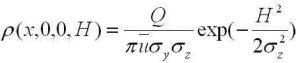函式可導性與連續性

函式可導性與連續性是可導函式的性質。

先看幾個定義：

（1）連續點：如果函式在某一鄰域內有定義，且x->x時limf(x)=f(x)，就稱x為f(x)的連續點。

一個推論，即y=f(x)在x處連續等價於y=f(x)在x處既左連續又右連續，也等價於y=f(x)在x處的左、右極限都等於f(x)。

這就包括了函式連續必須同時滿足三個條件：

（1）函式在x處有定義；

（2）x-> x時，limf(x)存在；

（3）x-> x時，limf(x)=f(x)。

初等函式在其定義域內是連續的。

（2）連續函式：函式f(x)在其定義域內的每一點都連續，則稱函式f(x)為連續函式。 （3）連續性與可導性關係：連續是可導的必要條件，即函式可導必然連續；不連續必然不可 導；連續不一定可導。典型例子：含尖點的連續函式