不連續性

在數學中，不連續性是函式的一種屬性。連續的函式是當輸入值的變化足夠小的時候，輸出的變化也會隨之足夠小的函式。如果輸入值的某種微小的變化會產生輸出值的一個突然的跳躍，甚至無法定義，則這個函式被稱為是不連續的函式，或者說具有不連續性 。

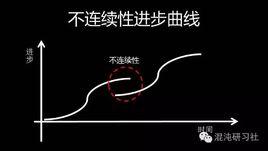
定義

不連續性

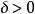不連續性

不連續性

若是一函式，定義域和值域都是實數，若存在自變數，存在，使得，有

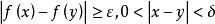不連續性

不連續性

則稱為不連續函式。換句話說，不論距固定點多近，都有距固定點更近的點使函式的值偏離固定點對應的值。例如狄利克雷函式就是一個處處不連續函式。

通過不連續函式的定義來了解不連續性是一個簡單直觀的方式。不連續性也套用在各種各樣的領域中，如物理學、醫學、經濟學等，在不同領域的概念也不盡相同。尤其是物理學中的量子力學，對不連續性的本質做了很好的詮釋 。

示例

量子（quantum）是現代物理的重要概念。最早是M·普朗克在1900年提出的。他假設黑體輻射中的輻射能量是不連續的，只能取能量基本單位的整數倍。後來的研究表明，不但能量表現出這種不連續的分離化性質，其他物理量諸如角動量、自旋、電荷等也都表現出這種不連續的量子化現象。這同以牛頓力學為代表的經典物理有根本的區別。量子化現象主要表現在微觀物理世界。描寫微觀物理世界的物理理論是量子力學。