非奇非偶函式

非奇非偶函式 如果對於函式定義域內的任意一個x，若f(-x)=-f(x)（奇函式）或f(-x)=f(x)（偶函式）都不能成立，那么函式f(x)既不是奇函式又不是偶函式，稱為非奇非偶函式。判斷函式奇偶性的第一步就是判斷函式的定義域是否關於數零對稱（這裡很多人不能理解，網上也經常有很多錯誤的實例，定義域應該關於數零對稱，並不是關於原點對稱，也不是關於y軸對稱），如果定義域不關於數零對稱那么顯然是非奇非偶函式。

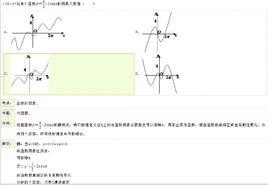
定義

當然，如果f(-x)=-f(x)和f(-x)=f(x)都能成立，

那么函式f(x)既是奇函式又是偶函式。

非奇非偶函式與既奇又偶函式的區別:

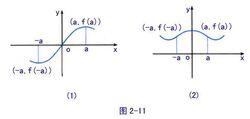
奇函式:

f(-x)=-f(x)

偶函式:

f(-x)=f(x)

既奇又偶函式:

非奇非偶函式

f(-x)=f(x) 和 f(-x)=-f(x)

非奇非偶函式:

存在X1,X2,使得:

f(-X1)不等於f(X1)

f(-X2)不等於-f(X2)

當然，定義域沒有與原點對稱的函式也是非奇非偶函式。

相關函式類型

奇函式：

f(-x)=-f(x)

偶函式：

f(-x)=f(x)

既奇又偶函式：

f(-x)=f(x) 和 f(-x)=-f(x)