簡介
 《九章算術》
《九章算術》 《九章算術》
《九章算術》根據研究,西漢的張蒼、耿壽昌曾經做過增補。最後成書最遲在東漢前期,但是其基本內容在東漢後期已經基本定型。《漢書藝文志》(班固根據劉歆《七略》寫成者)中著錄的數學書僅有《許商算術》、《杜忠算術》兩種,並無《九章算術》,可見《九章算術》的出現要晚於《七略》。《後漢書馬援傳》載其侄孫馬續“博覽群書,善《九章算術》”,馬續是公元1世紀最後二、三十年時人。再根據《九章算術》中可供判定年代的官名、地名等來推斷,現傳本《九章算術》的成書年代大約是在公元1世紀的下半葉。九章算術將書中的所有數學問題分為九大類,就是“九章”。
1984年,在湖北出土了《算數書》書簡。據考證,它比《九章算術》要早一個半世紀以上,書中有些內容和《九章算術》非常相似,一些內容的文句也基本相同。有人推測兩書具有某些繼承關係,但也有不同的看法認為《九章算術》沒有直接受到《算數書》影響。
後世的數學家,大都是從《九章算術》開始學習和研究數學,許多人曾為它作過注釋。其中最著名的有劉徽(263)、李淳風(656)等人。劉、李等人的注釋和《九章算術》一起流傳至今。唐宋兩代,《九章算術》都由國家明令規定為教科書。到了北宋,《九章算術》還曾由政府進行過刊刻(1084),這是世界上最早的印刷本數學書。在現傳本《九章算術》中,最早的版本乃是上述北宋本的南宋翻刻本(1213),現藏於上海圖書館(孤本,殘,只余前五卷)。清代戴震由《永樂大典》中抄出《九章算術》全書,並作了校勘。此後的《四庫全書》本、武英殿聚珍本、孔繼涵刻的《算經十書》本(1773)等,大多數都是以戴校本為底本的。
作為一部世界科學名著,《九章算術》在隋唐時期即已傳入朝鮮、日本。現在,它已被譯成日、俄、德、法等多種文字。
主要內容
《九章算術》的內容十分豐富,全書採用問題集的形式,收有246個與生產、生活實踐有聯繫的套用問題,其中每道題有問(題目)、答(答案)、術(解題的步驟,但沒有證明),有的是一題一術,有的是多題一術或一題多術。這些問題依照性質和解法分別隸屬於方田、粟米、衰(音崔cui)分、少廣、商功、均輸、盈不足、方程及勾股九章如下所示。原作有插圖,今傳本已只剩下正文了。
《九章算術》共收有246個數學問題,分為九章、它們的主要內容分別是:
第一章“方田”:田畝面積計算;提出了各種多邊形、圓、弓形等的面積公式;分數的通分、約分和加減乘除四則運算的完整法則。後者比歐洲早1400多年。
第二章“粟米”:穀物糧食的按比例折換;提出比例算法,稱為今有術;衰分章提出比例分配法則,稱為衰分術;
第三章“衰分”:比例分配問題;介紹了開平方、開立方的方法,其程式與現今程式基本一致。這是世界上最早的多位數和分數開方法則。它奠定了中國在高次方程數值解法方面長期領先世界的基礎。
第四章“少廣”:已知面積、體積,反求其一邊長和徑長等;
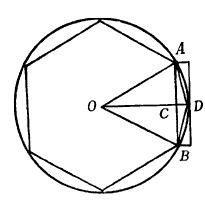 勾股定理求解
勾股定理求解第五章“商功”:土石工程、體積計算;除給出了各種立體體積公式外,還有工程分配方法;
第六章“均輸”:合理攤派賦稅;用衰分術解決賦役的合理負擔問題。今有術、衰分術及其套用方法,構成了包括今天正、反比例、比例分配、複比例、連鎖比例在內的整套比例理論。西方直到15世紀末以後才形成類似的全套方法。
第七章“盈不足”:即雙設法問題;提出了盈不足、盈適足和不足適足、兩盈和兩不足三種類型的盈虧問題,以及若干可以通過兩次假設化為盈不足問題的一般問題的解法。這也是處於世界領先地位的成果,傳到西方後,影響極大。
第八章“方程”:一次方程組問題;採用分離係數的方法表示線性方程組,相當於現在的矩陣;解線性方程組時使用的直除法,與矩陣的初等變換一致。這是世界上最早的完整的線性方程組的解法。在西方,直到17世紀才由萊布尼茲提出完整的線性方程的解法法則。這一章還引進和使用了負數,並提出了正負術——正負數的加減法則,與現今代數中法則完全相同;解線性方程組時實際還施行了正負數的乘除法。這是世界數學史上一項重大的成就,第一次突破了正數的範圍,擴展了數系。外國則到7世紀印度的婆羅摩及多才認識負數。
第九章“勾股”:利用勾股定理求解的各種問題。其中的絕大多數內容是與當時的社會生活密切相關的。提出了勾股數問題的通解公式:若a、b、c分別是勾股形的勾、股、弦,則,m>n。在西方,畢達哥拉斯、歐幾里得等僅得到了這個公式的幾種特殊情況,直到3世紀的丟番圖才取得相近的結果,這已比《九章算術》晚約3個世紀了。勾股章還有些內容,在西方卻還是近代的事。例如勾股章最後一題給出的一組公式,在國外到19世紀末才由美國的數論學家迪克森得出。
主要特點
《九章算術》確定了中國古代數學的框架,
 《九章算術》
《九章算術》然而,《九章算術》亦有其不容忽視的缺點:沒有任何數學概念的定義,也沒有給出任何推導和證明。魏景元四年(263年),劉徽給《九章算術》作注,才大大彌補了這個缺陷。
劉徽是中國數學家之一。他的生平現在知之甚少。據考證,他是山東鄒平人。劉徽定義了若干數學概念,全面論證了《九章算術》的公式解法,提出了許多重要的思想、方法和命題,他在數學理論方面成績斐然。
劉徽對數學概念的定義抽象而嚴謹。他揭示了概念的本質,基本符合現代邏輯學和數學對概念定義的要求。而且他使用概念時亦保持了其同一性。如他提出凡數相與者謂之率,把率定義為數量的相互關係。又如他把正負數定義為今兩算得失相反,要令正負以名之,擺脫了正為余,負為欠的原始觀念,從本質上揭示了正負數得失相反的相對關係。
《九章算術》的算法儘管抽象,但相互關係不明顯,顯得零亂。劉徽大大發展深化了中算中久已使用的率概念和齊同原理,把它們看作運算的綱紀。許多問題,只要找出其中的各種率關係,通過乘以散之,約以聚之,齊同以通之,都可以歸結為今有術求解。
一平面(或立體)圖形經過平移或鏇轉,其面積(或體積)不變。把一個平面(或立體)圖形分解成若干部分,各部分面積(或體積)之和與原圖形面積(或體積)相等。基於這兩條不言自明的前提的出入相補原理,是中國古代數學進行幾何推演和證明時最常用的原理。劉徽發展了出入相補原理,成功地證明了許多面積、體積以及可以化為面積、體積問題的勾股、開方的公式和算法的正確性。
數學成就
 《九章算術》
《九章算術》《九章算術方程》章共18問,全都是一次方程組問題,未知數最多時可達五個。其解法,首先以豎行用算籌列出各方程的係數,如“方程”章第一題,它相當於求解:
3x+2+=39,(1)
2x+3+=34,(2)
x+2+3=26。(3)
列出的籌式如
123
232
311
263439,
豎行,即相當於上面的式(1)、(2)、(3)。其消元方法就是令左右行連續相減(如以3乘再連續減即可消去x項係數)。“程”是指“計算”、“方”是指這樣列出的籌式是方形的,這才是“方程”這一數學術語的原意。《九章算術》中的這項成果,比世界其它國家和地區的同類成果要早很多年。“方程”章還在世界數學史上首次引入了負數及其加減法運算法則。
在《九章算術》中,開平方和開立方時所列籌式以及演算過程,其意義和求解x=、x=的數值解法是相同的。這樣,在開平方的過程中便可很自然地引出一般二次方程的解法。由此出發,更開宋元時期高次方程數值解法的先聲。
歷史影響
 劉徽
劉徽關於對《九章算術》所做的注住要有:三國時曹魏劉徽注,唐朝李淳風注,南宋楊輝著《詳解九章算法》選用《九章算術》中80道典型的題作過詳解並分類,清李潢(?~1811年)所著《九章算術細草圖說》對《九章算術》進行了校訂、列算草、補插圖、加說明,尤其是圖文並茂之作。現代錢寶琮(1892~1974年)曾對包括《九章算術》在內的《算經十書》進行了校點,用通俗語言、近代數學術語對《九章算術》及劉、李注文詳加注釋。80年代以來,今人白尚恕、郭書春、李繼閔等都有校注本出版。
《九章算術》是世界上最早系統敘述了分數運算的著作;其中盈不足的算法更是一項令人驚奇的創造;“方程”章還在世界數學史上首次闡述了負數及其加減運算法則。在代數方面,《九章算術》在世界數學史上最早提出負數概念及正負數加減法法則;現在中學講授的線性方程組的解法和《九章算術》介紹的方法大體相同。注重實際套用是《九章算術》的一個顯著特點。該書的一些知識還傳播至印度和阿拉伯,甚至經過這些地區遠至歐洲。
《九章算術》是幾代人共同勞動的結晶,它的出現標誌著中國古代數學體系的形成.後世的數學家,大都是從《九章算術》開始學習和研究數學知識的。唐宋兩代都由國家明令規定為教科書。1084年由當時的北宋朝廷進行刊刻,這是世界上最早的印刷本數學書。可以說,《九章算術》是中國為數學發展做出的又一傑出貢獻。
後世影響
《九章算術》是世界上最早系統敘述了分數運算的著作;其中盈不足的算法更是一項令人驚奇的創造;“方程”章還在世界數學史上首次闡述了負數及其加減運算法則。在代數方面,《九章算術》在世界數學史上最早提出負數概念及正負數加減法法則;現在中學講授的線性方程組的解法和《九章算術》介紹的方法大體相同。注重實際套用是《九章算術》的一個顯著特點。該書的一些知識還傳播至印度和阿拉伯,甚至經過這些地區遠至歐洲。《九章算術》是幾代人共同勞動的結晶,它的出現標誌著中國古代數學體系的形成.後世的數學家,大都是從《九章算術》開始學習和研究數學知識的。唐宋兩代都由國家明令規定為教科書。1084年由當時的北宋朝廷進行刊刻,這是世界上最早的印刷本數學書。
所以,《九章算術》是中國為數學發展做出的一傑出貢獻。

