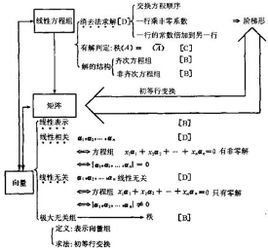
簡介
xj表未知量,aij稱係數,bi稱常數項。
稱為係數矩陣和增廣矩陣。若x1=c1,x2=c2,…,xn=cn代入所給方程各式均成立,則稱(c1,c2,…,cn)為一個解。若c1,c2,…,cn不全為0,則稱(c1,c2,…,cn)為非零解。若常數項均為0,則稱為齊次線性方程組,它總有零解(0,0,…,0)。兩個方程組,若它們的未知量個數相同且解集相等,則稱為同解方程組。線性方程組主要討論的問題是:①一個方程組何時有解。②有解方程組解的個數。③對有解方程組求解,並決定解的結構。這幾個問題均得到完滿解決:所給方程組有解,則秩(A)=秩(增廣矩陣);若秩(A)=秩=r,則r=n時,有唯一解;r
當非齊次線性方程組有解時,解唯一的充要條件是對應的齊次線性方程組只有零解;解無窮多的充要條件是對應齊次線性方程組有非零解。但反之當非齊次線性方程組的導出組僅有零解和有非零解時,不一定原方程組有唯一解或無窮解,事實上,此時方程組不一定有 ,即不一定有解。
克萊姆法則(見行列式)給出了一類特殊線性方程組解的公式。n個未知量的任一齊次方程組的解集均構成n維空間的一個子空間。
線性方程組有廣泛套用,熟知的線性規劃問題即討論對解有一定約束條件的線性方程組問題。
解法
①克萊姆法則.用克萊姆法則求解方程組 有兩個前提,一是方程的個數要等於未知量的個數,二是係數矩陣的行列式要不等於零。用克萊姆法則求解方程組實際上相當於用逆矩陣的方法求解線性方程組,它建立線性方程組的解與其係數和常數間的關係,但由於求解時要計算n+1個n階行列式,其工作量常常很大,所以克萊姆法則常用於理論證明,很少用於具體求解。
②矩陣消元法.將線性方程組的增廣矩陣通過行的初等變換化為行簡化階梯形矩陣 ,則以行簡化階梯形矩陣為增廣矩陣的線性方程組與原方程組同解。當方程組有解時,將其中單位列向量對應的未知量取為非自由未知量,其餘的未知量取為自由未知量,即可找出線性方程組的解。
關於未知量是一次的方程組,其一般形式為
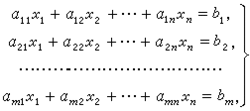 ⑴
⑴式中x1,x2,…,xn代表未知量,αij(1≤i≤m,1≤j≤n)稱為方程⑴的係數,bi(1≤i≤m)稱為常數項。係數和常數項都是任意的複數或某一個域的元素。
當常數項b1,b2,…,bn都等於零時,則方程組⑴稱為齊次線性方程組。
方程組⑴的係數所構成的m行n列矩陣
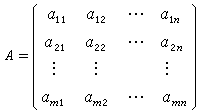 線性方程組
線性方程組稱為方程組⑴的係數矩陣。在A中添加由常數項組成的列而得到一個m行n+1列矩陣
 線性方程組
線性方程組稱為方程組⑴的增廣矩陣。
如果在方程組⑴中,以一組複數或域F的元素с1,с2,…,сn代替未知量x1,x2,…,xn,每一個方程的兩端相等,那么с1,с2,…,сn稱為方程組⑴的一個解。
關於線性方程組,有以下主要結果。
①線性方程組⑴有解的充分必要條件是,係數矩陣A與增廣矩陣都有相同的秩。
②在A與都有相同的秩r>0的情形下,A有一個r階子式D不等於零,設
 線性方程組
線性方程組於是方程組⑴與僅含有前r個方程的方程組同解。可將前r個方程改寫為
 ⑵
⑵方程組⑵的一般解公式為x1=D1/D,x2=D2/D,…,xr=Dr/D,⑶
式中Dj(j=1,2,…,r)是把D的第j列換成方程組⑵的右端的列所得到的一個r階行列式,即
 線性方程組
線性方程組因而x1,x2,…,xr可由其餘的未知量xr+1,xr+2,…,xn線性表出,xr+1,xr+2,…,xn稱為自由未知量。
當r