定義
費波那契數列（義大利語：Successione di Fibonacci），又譯為 費波拿契數、 斐波那契數列、 費氏數列、 黃金分割數列。
在數學上， 費波那契數列是以遞歸的方法來定義：
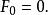Fibonacci數列
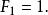Fibonacci數列
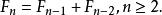Fibonacci數列用文字來說，就是費波那契數列由0和1開始，之後的費波那契係數就是由之前的兩數相加而得出。首幾個費波那契係數是：
0,1,1,2,3,5,8,13,21,34,55,89,144,233……（OEIS中的數列A000045）
特別指出：0不是第一項，而是第零項。
源起
根據高德納（Donald Ervin Knuth）的《電腦程式設計藝術》（ The Art of Computer Programming）， 1150年印度數學家Gopala和金月在研究箱子包裝物件長寬剛好為1和2的可行方法數目時，首先描述這個數列。在西方，最先研究這個數列的人是比薩的列奧那多（義大利人斐波那契Leonardo Fibonacci），他描述兔子生長的數目時用上了這數列:
•第一個月初有一對剛誕生的兔子
•第二個月之後（第三個月初）它們可以生育
•每月每對可生育的兔子會誕生下一對新兔子
•兔子永不死去
假設在n月有兔子總共a對，n+1月總共有b對。在n+2月必定總共有a+b對：因為在n+2月的時候，前一月（n+1月）的b對兔子可以存留至第n+2月（在當月屬於新誕生的兔子尚不能生育）。而新生育出的兔子對數等於所有在n月就已存在的a對。
與黃金分割
克卜勒發現數列前、後兩項之比1/2 ,2/3 , 3/5 ,5/8 ,8/13 ,13/21 ,21/34 ,...... ,也組成了一個數列，會趨近黃金分割：
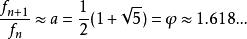Fibonacci數列斐波那契數亦可以用連分數來表示：
Fibonacci數列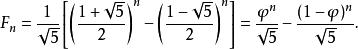
Fibonacci數列而黃金分割數亦可以用無限連分數表示：
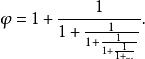Fibonacci數列而黃金分割數也可以用無限多重根號表示：
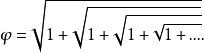Fibonacci數列和自然的關係
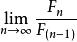Fibonacci數列
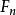Fibonacci數列許多的生物構成都和斐波那契數列有正相關。例如人體從腳底至頭頂之距離和從肚臍至腳底之距趨近於,向日葵的種子螺旋排列有99%是。
恆等式
證明以下的恆等式有很多方法。以下會用組合論述來證明。
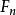Fibonacci數列可以表示用多個1和多個2相加令其和等於n的方法的數目。
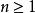Fibonacci數列 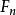Fibonacci數列
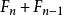Fibonacci數列不失一般性，我們假設，F是計算了將1和2加到n的方法的數目。若第一個被加數是1，有種方法來完成對n-1的計算；若第一個被加數是2，有F來完成對n-2的計算。因此，共有種方法來計算n的值。
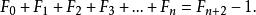Fibonacci數列計算用多個1和多個2相加令其和等於n+1的方法的數目，同時至少一個加數是2的情況。
如前所述，當n>0，有F種這樣的方法。因為當中只有一種方法不用使用2，就即1+1+...+1（n+1項），於是我們從 F減去1。
若第1個被加數是2，有 F種方法來計算加至n-1的方法的數目；
若第2個被加數是2、第1個被加數是1，有F種方法來計算加至 n-2的方法的數目。
重複以上動作。
若第n+1個被加數為2，它之前的被加數均為1，就有F種方法來計算加至0的數目。
1.若第1個被加數是2，有 F種方法來計算加至n-1的方法的數目；
2.若第2個被加數是2、第1個被加數是1，有F種方法來計算加至 n-2的方法的數目。
3.重複以上動作。
4.若第n+1個被加數為2，它之前的被加數均為1，就有F種方法來計算加至0的數目。
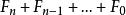Fibonacci數列若該數式包含2為被加數，2的首次出現位置必然在第1和n+1的被加數之間。2在不同位置的情況都考慮到後，得出為要求的數目。
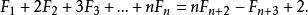Fibonacci數列
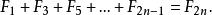Fibonacci數列
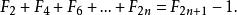Fibonacci數列
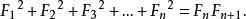Fibonacci數列
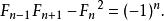Fibonacci數列相關的數列
反費波那西
反費波那西數列的遞歸公式如下：
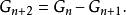Fibonacci數列如果它以1,-1，之後的數是：1,-1,2,-3,5,-8, ...
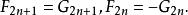Fibonacci數列即是。
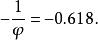Fibonacci數列反費波那西數列兩項之間的比會趨近。
巴都萬數列
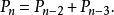Fibonacci數列費波那西數列可以用一個接一個的正方形來表現，巴都萬數列則是用一個接一個的等邊三角形來表現，它有的關係。
套用
1970年，尤里·馬季亞謝維奇指出了偶角標的斐波那契函式
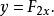Fibonacci數列正是滿足Julia Robison假設的丟番圖函式，因而證明了希爾伯特第十問題是不可解的。
相關猜想
斐波那契數列中是否存在無窮多個素數？
在斐波那契數列中，有素數： 2, 3, 5, 13, 89, 233, 1597, 28657, 514229, 433494437, 2971215073, 99194853094755497, 1066340417491710595814572169, 19134702400093278081449423917…… 目前已知最大素數是第81839個斐波那契數，一共有17103位數。
