裴波那契數列的來歷
“斐波那契數列”的發明者,是義大利數學家列昂納多•斐波那契(LeonardoFibonacci,生於公元1170年,卒於1240年,籍貫大概是比薩)。他被人稱作“比薩的列昂納多”。1202年,他撰寫了《珠算原理》(LiberAbaci)一書。他是第一個研究了印度和阿拉伯數學理論的歐洲人。他的父親被比薩的一家商業團體聘任為外交領事,派駐地點相當於今日的阿爾及利亞地區,列昂納多因此得以在一個阿拉伯老師的指導下研究數學。他還曾在埃及、敘利亞、希臘、西西里和普羅旺斯研究數學。
13 世紀初,歐洲最好的數學家是斐波拉契,他寫了一本叫做《算盤書》的著作,是當時歐洲最好的數學書。書中有著許多有趣的數學題,其中有這樣的一題:
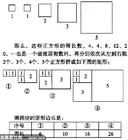
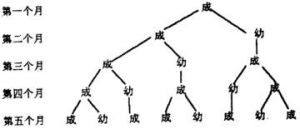
如果一對兔子每月能生一對小兔子,而每對小兔在它出生後的第 3 個月裡,又能開始生一對小兔子,假定在不發生死亡的情況下,由一對初生的兔子開始,一年後能繁殖成多少對兔子?
推算一下兔子的對數是很有意思的。為了敘述得有條理,我們假設最初的一對兔子出生在頭一年的 12 月份。顯然, 1 月份只有一對兔子,到 2 月份時,這對兔子生了 1 對小兔子,總共 2 對兔子;在 3 月份里,這對兔子又生了一對小兔,總共 3 對兔子;到 4 月份, 2 月份生的兔子開始生小兔了,這個月生了 2 對小兔,所以總共 5 對兔子;在 5 月份里,不僅最初的那對兔子和 2 月份出生的兔子各生了一對小兔, 2 月份出生的兔子也生了 1 對小兔,總共出生了 3 對兔子,所以總共 8 對兔子……。
照這樣推算下去,當然能得到題目的答案,不過,斐波拉契對這種算法很不滿意,他覺得這種方法太繁瑣了而且推算到最後情況複雜,稍有不慎就會出現差錯。於是他又深入探索了題目中的數量關係,終於找到了一種簡捷的解題方法。
斐波拉契把推算得到的頭幾個數擺成一串。
1 , 1 , 2 , 3 , 5 , 8 ,……
這串數里隱含著一個規律,從第 3 個數開始,後面的每個數都是它前面兩個數的和。根據這個規律,只要作一些簡單的加法,就能推算出以後各個月兔子的數目了。
這樣,要知道一年後兔子的對數是多少,也就是看這串數的第 13 個數是多少。由 5 + 8 = 13 , 8 + 13 = 21 , 13 + 21 = 34 , 21 + 34 = 55 , 34 + 55 = 89 , 55 + 89 = 144 , 89 + 144 = 233 ,可知題目的答案是 233 對。
按照這個規律推算出來的數,構成了數學史上有名的數列。大家都叫它“斐波拉契數列”。這個數列有許多奇特的性質,例如,從第 3 個數起,每個數與它後面那個數的比值,都很接近於 0.618,正好與大名鼎鼎的“黃金分割”相吻合。人們還發現,連一些生物的生長規律,在某種假定下也可由這個數列來刻畫呢。
你可以通過這個連結引用該篇文章
http://xuyaaiwinnie.bokee.com/tb.b?diaryId=13389151