基本介紹
廣義斐波那契序列由遞推關係
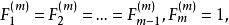廣義Fibonacci數列
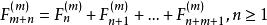廣義Fibonacci數列所產生的序列 ，稱為m級廣義斐波那契序列，其通項表達式為
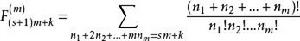廣義Fibonacci數列
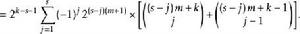廣義Fibonacci數列式中s=0，1，2，…;k=1，2，…，m。設ω為方程
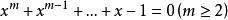廣義Fibonacci數列的惟一正根，則
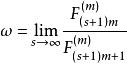廣義Fibonacci數列相關介紹
定義及通項表達式
人們對Fibonacci數列的研究興趣歷時幾百年而不衰，後來又將這個數列進行推廣，得到了廣義Fibonacci數列。2004 年，馬巧雲利用生成函式得出了廣義Fibonacci數列的一個通項表達式。
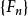廣義Fibonacci數列廣義Fibonacci數列 由如下的遞推公式給出:
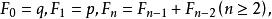廣義Fibonacci數列特別的當q=0,p= 1時，記作{f}，稱為熟知的Fibonacci數列。其通項公式為:
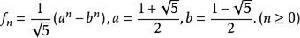廣義Fibonacci數列當q=2,p=1時記作{L}稱為Lucas數列。其通項公式為:
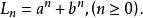廣義Fibonacci數列 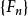廣義Fibonacci數列廣義Fibonacci數列 與Fibonacci數列{f}符合如下的關係式
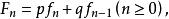廣義Fibonacci數列
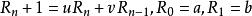廣義Fibonacci數列著名的Fibonacci數列有許多通項表達式和性質。陳淑貞，曾慶年利用數學歸納法和特徵方程求根的方法對廣義Fibonacci數列 進行研究，得到了兩個通項表達式和一個性質 。
周期性
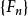廣義Fibonacci數列Wall D D1960年證明了廣義Fibonacci數列 以任意正整數為模的模數列是周期數列，袁明豪在2007年也得到了類似結論。
黃金分割數
吳強將Fibonacci數列進行了推廣，利用生成函式的方法得出廣義Fibonacci數列的通項及廣義Fibonacci數列任意相鄰四項之間的關係，討論了這種數列的前後項之比的收斂性及極限仍然為黃金分割數 。
