定義
 遞歸數列
遞歸數列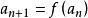 遞歸數列
遞歸數列 遞歸數列
遞歸數列給定 ,由遞歸公式 由前項定義後項所得到的數列 稱為遞歸定義數列,簡稱為遞歸數列(recursive sequence )。
等差數列
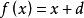 遞歸數列
遞歸數列 遞歸數列
遞歸數列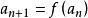 遞歸數列
遞歸數列 遞歸數列
遞歸數列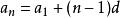 遞歸數列
遞歸數列若遞歸函式為 ,那么給定 後,由遞歸公式 定義出來的數列 是等差數列,容易求出其通項公式為 。
等比數列
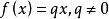 遞歸數列
遞歸數列 遞歸數列
遞歸數列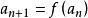 遞歸數列
遞歸數列 遞歸數列
遞歸數列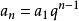 遞歸數列
遞歸數列若遞歸函式為 ,那么給定 ,由遞歸公式 定義出來的數列 是等比數列,容易求出其通項公式為 。
一階線性遞歸數列
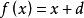 遞歸數列
遞歸數列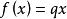 遞歸數列
遞歸數列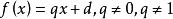 遞歸數列
遞歸數列等差數列、等比數列對應的特殊的遞歸函式 、 ,比這些稍複雜一點的是普通的一元線性函式 定義的遞歸數列。
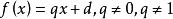 遞歸數列
遞歸數列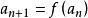 遞歸數列
遞歸數列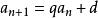 遞歸數列
遞歸數列 遞歸數列
遞歸數列 遞歸數列
遞歸數列若遞歸函式為一元線性函式 ,那么由遞歸公式 ,即 定義的數列 稱為 一階線性遞歸數列,在給定 後,如何求出定義出來的一階線性遞歸數列的通項呢?一般有兩種做法:
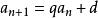 遞歸數列
遞歸數列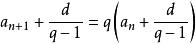 遞歸數列
遞歸數列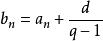 遞歸數列
遞歸數列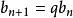 遞歸數列
遞歸數列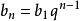 遞歸數列
遞歸數列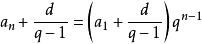 遞歸數列
遞歸數列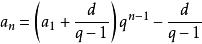 遞歸數列
遞歸數列(1)我們可以將 拆項相湊改寫為 ,若記 ,這就成為了遞歸等比數列的遞歸模式 了。由 ,即 ,可得 。
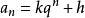 遞歸數列
遞歸數列 遞歸數列
遞歸數列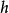 遞歸數列
遞歸數列(2)也可以在猜測 後,通過待定係數法求出 和 ,再用數學歸納法證明。
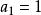 遞歸數列
遞歸數列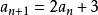 遞歸數列
遞歸數列例1 給定 ,求由一階線性遞歸公式 定義的數列的通項。
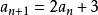 遞歸數列
遞歸數列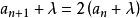 遞歸數列
遞歸數列 遞歸數列
遞歸數列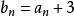 遞歸數列
遞歸數列解法1將 改寫為 ,顯然應該取 ,記 ,
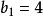 遞歸數列
遞歸數列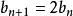 遞歸數列
遞歸數列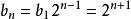 遞歸數列
遞歸數列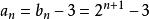 遞歸數列
遞歸數列則有 , 。所以 ,最後可得
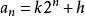 遞歸數列
遞歸數列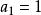 遞歸數列
遞歸數列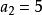 遞歸數列
遞歸數列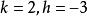 遞歸數列
遞歸數列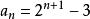 遞歸數列
遞歸數列解法2猜測 ,由 , ,通過待定係數法求出 ,即 。下面用數學歸納法證明。
 遞歸數列
遞歸數列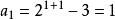 遞歸數列
遞歸數列初始驗證: 時, ,符合通項公式。
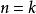 遞歸數列
遞歸數列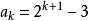 遞歸數列
遞歸數列通項假定:設 時結論成立,即 ,
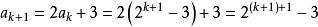 遞歸數列
遞歸數列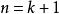 遞歸數列
遞歸數列漸進遞推: ,即 時結論也成立。
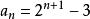 遞歸數列
遞歸數列所以 確為所求之通項公式。
非線性遞歸
有很多非常有趣的數學問題可以歸結為遞歸數列,但其對應的遞歸函式不一定都是線性函式,在研究其收斂性時也未必要把通項求出來。
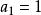 遞歸數列
遞歸數列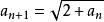 遞歸數列
遞歸數列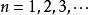 遞歸數列
遞歸數列 遞歸數列
遞歸數列例1 已知 , , ,試證明由此遞歸定義的數列 收斂,並求其極限。
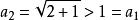 遞歸數列
遞歸數列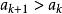 遞歸數列
遞歸數列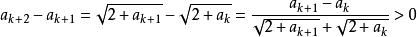 遞歸數列
遞歸數列解 利用數學歸納法可以證明數列單調增加,事實上 ,設 ,那么 。
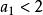 遞歸數列
遞歸數列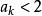 遞歸數列
遞歸數列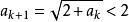 遞歸數列
遞歸數列再利用數學歸納法可以證明數列有上界,事實上 ,設 ,那么 。
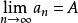 遞歸數列
遞歸數列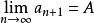 遞歸數列
遞歸數列根據單調有界數列必收斂,可設 ,且必有 ,
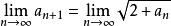 遞歸數列
遞歸數列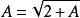 遞歸數列
遞歸數列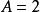 遞歸數列
遞歸數列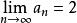 遞歸數列
遞歸數列從而由 可得 ,得唯一正數解 ,即 。
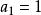 遞歸數列
遞歸數列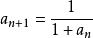 遞歸數列
遞歸數列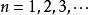 遞歸數列
遞歸數列 遞歸數列
遞歸數列例2已知 , , ,試證明由此遞歸定義的數列 收斂,並求其極限 。
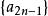 遞歸數列
遞歸數列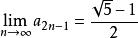 遞歸數列
遞歸數列解利用數學歸納法可以證明數列子數列 單調減少有下界0,有 。
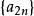 遞歸數列
遞歸數列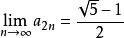 遞歸數列
遞歸數列利用數學歸納法可以證明數列子數列 單調增加有上界1,有 。
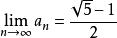 遞歸數列
遞歸數列所以 。
一階線性差分方程
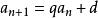 遞歸數列
遞歸數列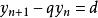 遞歸數列
遞歸數列一階線性遞歸數列的遞歸關係式 ,對應了一個一階線性非齊次差分方程 ,一階線性非齊次差分方程的解法本質上就是體現了求一階線性遞歸數列通項的方法 。
二階線性齊次遞歸數列
 遞歸數列
遞歸數列例3 設x1=3,x2=7,x(n+2)=5x(n+1)-6Xn,求數列 的通項。
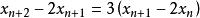 遞歸數列
遞歸數列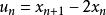 遞歸數列
遞歸數列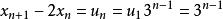 遞歸數列
遞歸數列解 將遞歸定義式改寫為 ,可知數列 是以3為公比的等比數列,由此可求得 ,
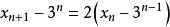 遞歸數列
遞歸數列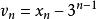 遞歸數列
遞歸數列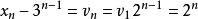 遞歸數列
遞歸數列再改寫為 ,可知數列 是等比數列,由此可求得 。
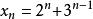 遞歸數列
遞歸數列最後可得數列通項為 。
本例解法具有較普遍一類問題具有典型意義及推廣價值。
例4 ( 斐波那契數列)設F1=1,F2=1,F(n+2)=F(n+1)+Fn ,求數列{Fn} 的通項 。
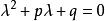 遞歸數列
遞歸數列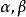 遞歸數列
遞歸數列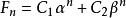 遞歸數列
遞歸數列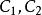 遞歸數列
遞歸數列分析與解 斐波那契數列是一個非常典型的二階遞歸數列,這類 二階線性齊次遞歸數列問題的解法,可由本詞條 例3的解法得到啟發,若方程(特徵方程) 有兩個不相等的實數解(特徵根) ,則由二階線性齊次式F(n+2)+pF(n+1)+qFn=0遞歸定義數列的通項為 ,其中待定常數 由給定的兩個初始項確定。
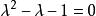 遞歸數列
遞歸數列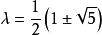 遞歸數列
遞歸數列這裡斐波那契數列對應的特徵方程為 ,特徵根為 。所以可得
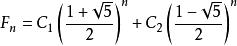 遞歸數列
遞歸數列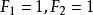 遞歸數列
遞歸數列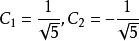 遞歸數列
遞歸數列,根據 ,可確定出 ,即
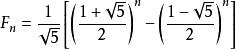 遞歸數列
遞歸數列遞歸數列極限
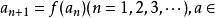 遞歸數列
遞歸數列設 區間I,若f(x)在區間I單調上升,a>a(a<a) ,則數列{a}單調上升(單調下降);若f(x)在區間I單調下降,則數列{a}不具單調性。
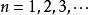 遞歸數列
遞歸數列證:設f(x)在區間I單調上升,由a>a得到f(a)>f(a) ,即a>a 。若a>a ,則f(a)>f(a) ,即a>a 。因此對於 有a>a ,即數列{a}單調上升。當a<a 時同樣可證數列{a}單調下降。另一結論類似可證。

