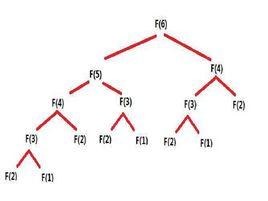
遞歸
程式調用自身的編程技巧稱為遞歸( recursion)。遞歸做為一種算法在程式設計語言中廣泛套用。 一個過程或函式在其定義或說明中有直接或間接調用自身的一種方法,它通常把一個大型複雜的問題層層轉化為一個與原問題相似的規模較小的問題來求解,遞歸策略只需少量的程式就可描述出解題過程所需要的多次重複計算,大大地減少了程式的代碼量。遞歸的能力在於用有限的語句來定義對象的無限集合。一般來說,遞歸需要有邊界條件、遞歸前進段和遞歸返回段。當邊界條件不滿足時,遞歸前進;當邊界條件滿足時,遞歸返回。
遞歸,就是在運行的過程中調用自己。
構成遞歸需具備的條件:
1,子問題須與原始問題為同樣的事,且更為簡單;
2,不能無限制地調用本身,須有個出口,化簡為非遞歸狀況處理。
在數學和計算機科學中,遞歸指由一種(或多種)簡單的基本情況定義的一類對象或方法,並規定其他所有情況都能被還原為其基本情況。
遞推公式
如果數列{an}的第n項與它前一項或幾項的關係可以用一個式子來表示,那么這個公式叫做這個數列的遞推公式。
由遞推公式寫出數列的方法:
1,根據遞推公式寫出數列的前幾項,依次代入計算即可
2,若知道的是末項,通常將所給公式整理成用後面的項表示前面的項的形式。
遞歸公式簡介
遞歸公式屬於遞推公式,這樣一個數列可以有三種給出的方法。
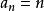 遞歸公式
遞歸公式例如自然數列用通項公式表示為:;
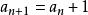 遞歸公式
遞歸公式用遞推公式表示為:,初始條件為a1=1;
 遞歸公式
遞歸公式用遞歸公式表示為:,初始條件,a1=1,a2=2;
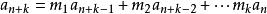 遞歸公式
遞歸公式線性遞歸公式:遞歸公式的各項的次數均為一次時,便稱為線性遞歸公式。用連續k項的表達式來表示緊接的後一項的線性遞歸公式叫做k階線性遞歸公式,其一般形式如下:。
在程式設計的套用
遞歸程式處理的問題是程式設計中經常遇到的問題,這類問題通常可以分為兩類:第一類是數學上的遞歸函式,要求算得一個函式值,例如階乘函式和勒讓德多項式函式;第二類問題具有遞歸特徵,目的是求出滿足某種條件的操作序列,例如漢諾塔問題和八皇后問題。第一類問題的程式設計是簡單的、機械的,而第二類問題則不然,由於涉及面廣,沒有統一的規則可循,所以編程過程往往比較複雜,而且編得的程式不大好理解。究其原因在於,第一類問題已經有了現成的函式公式,第二類則沒有。如果對第二類問題也能寫出它的遞歸公式,那么編碼過程就會大大簡化,而且還可以改善程式的可讀。
遞歸程式設計的公式化方法是一種簡單而有效的設計思想,它把程式設計和程式理解的難點都集中到遞歸公式上。陸登波通過舉例證明這種思想能夠簡化程式設計,而且得到的程式顯然好於通常的程式。這種思想有普遍性,適用於多數遞歸程式的設計。由遞歸公式設計出的程式具有標準的分支結構,編寫和理解都要簡單的多。