正文
經典分析學處理問題往往泛言或零散地看待所考慮的函式。雖有時取符合於某種規定的函式類X,但沒有明確地把X當作幾何的對象。現代分析學的一般方法在於視Ω為拓撲空間或測度空間又以問題的需要規定類中映射(即函式):Ω→A滿足的條件,諸如連續性、有界性、可測性、可微性、可積性等;從幾何學、拓撲學及代數學的角度,對X一方面賦與關於加法與數量乘法的封閉性,這裡加法為:ƒ∈X,g∈X→ƒ+g∈X,(ƒ+g)(x)=ƒ(x)+ g(x),凬x∈Ω;數量乘法為:ƒ∈X,λ∈A→λƒ∈X,(λƒ)(x)=λƒ(x),凬x∈Ω(即X對通常函式的線性運算封閉);另一方面使之成為拓撲空間,且兩方面又滿足一定的要求(例如線性運算關於拓撲是連續的等)。這樣,函式空間X通常也是拓撲線性空間。經典分析學研究中出現了許多重要的函式空間。對一些類型的函式空間,現已取得相當豐富的理論成就。當Ω是拓撲空間,Ω上有界連續函式全體以極大模
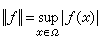 為範數時構成巴拿赫空間C(Ω)。特別當Ω是局部緊的,C(Ω)中具緊支集(函式ƒ的支集即集合{x∈Ω;ƒ(x)≠0}的閉包)的函式全體C0(Ω)是C(Ω)一個不完備的線性子空間。當Ω是緊的,Ω上所有連續函式必有界,它們就構成C(Ω)。對緊空間Ω的特例
為範數時構成巴拿赫空間C(Ω)。特別當Ω是局部緊的,C(Ω)中具緊支集(函式ƒ的支集即集合{x∈Ω;ƒ(x)≠0}的閉包)的函式全體C0(Ω)是C(Ω)一個不完備的線性子空間。當Ω是緊的,Ω上所有連續函式必有界,它們就構成C(Ω)。對緊空間Ω的特例 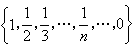 ,
,
當在Ω中定義了測度μ,在(Ω,μ)上可測並使
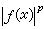 在Ω上可積(1≤p<∞)的函式ƒ的全體,賦有範數
在Ω上可積(1≤p<∞)的函式ƒ的全體,賦有範數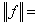
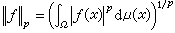 時構成巴拿赫空間即勒貝格空間lp(Ω,μ)。lp(Ω,μ)中序列{ƒn}收斂(稱為p次平均收斂)到ƒ 即指
時構成巴拿赫空間即勒貝格空間lp(Ω,μ)。lp(Ω,μ)中序列{ƒn}收斂(稱為p次平均收斂)到ƒ 即指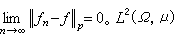 是一希爾伯特空間,ƒ,g∈l2(Ω,μ)的內積
是一希爾伯特空間,ƒ,g∈l2(Ω,μ)的內積 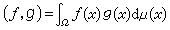 ,在復值函式情況下l2(Ω,μ)的內積為
,在復值函式情況下l2(Ω,μ)的內積為 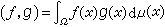 。
。
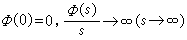 。命lφ(Ω,μ)表所有使φ(|ƒ(x)|)在 Ω上可積的函式ƒ(x)。若存在某固定的C>0,φ(2s)≤Cφ(s),則對某k>0使φ(k|ƒ(x)|)可積的函式 ƒ全體所成集合 L
。命lφ(Ω,μ)表所有使φ(|ƒ(x)|)在 Ω上可積的函式ƒ(x)。若存在某固定的C>0,φ(2s)≤Cφ(s),則對某k>0使φ(k|ƒ(x)|)可積的函式 ƒ全體所成集合 L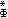 (Ω,μ)取範數
(Ω,μ)取範數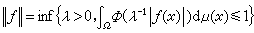 時成為一個巴拿赫空間,稱為奧爾里奇空間。當φ(s)=sp(1<p<∞)時就給出奧爾里奇空間的特殊情形lp(Ω,μ)。如果存在正數α使|ƒ(x)|≤α幾乎處處成立(即除去一個零測度集外都成立), 稱ƒ 為(Ω,μ)上本質有界可測函式,所有這樣函式ƒ在取本質上界
時成為一個巴拿赫空間,稱為奧爾里奇空間。當φ(s)=sp(1<p<∞)時就給出奧爾里奇空間的特殊情形lp(Ω,μ)。如果存在正數α使|ƒ(x)|≤α幾乎處處成立(即除去一個零測度集外都成立), 稱ƒ 為(Ω,μ)上本質有界可測函式,所有這樣函式ƒ在取本質上界 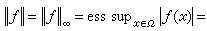
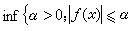 (幾乎處處)}為範數時構成巴拿赫空間M(Ω,μ)。對Ω是每點具有單位質量(即測度為1)的序列{1, 2,3,…,n}所成離散空間,M(Ω,μ)及lp(Ω,μ)(1<p<∞)分別就是熟知的序列空間m及lp。當(Ω,μ)的全空間Ω有有窮的測度時, 還可定義又一重要函式空間S(Ω,μ), S(Ω,μ)表示所有Ω上幾乎處處有窮的可測函式ƒ,它是以
(幾乎處處)}為範數時構成巴拿赫空間M(Ω,μ)。對Ω是每點具有單位質量(即測度為1)的序列{1, 2,3,…,n}所成離散空間,M(Ω,μ)及lp(Ω,μ)(1<p<∞)分別就是熟知的序列空間m及lp。當(Ω,μ)的全空間Ω有有窮的測度時, 還可定義又一重要函式空間S(Ω,μ), S(Ω,μ)表示所有Ω上幾乎處處有窮的可測函式ƒ,它是以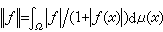 為擬範數的弗雷歇空間,其中序列{ƒn}收斂於ƒ,即
為擬範數的弗雷歇空間,其中序列{ƒn}收斂於ƒ,即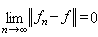 ,若且唯若
,若且唯若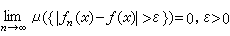 (即依測度收斂)。特別當Ω=(1,2,…,n,…)在點n有質量1/2n時,S(Ω)成為序列空間s。
(即依測度收斂)。特別當Ω=(1,2,…,n,…)在點n有質量1/2n時,S(Ω)成為序列空間s。 在複平面C 的區域 Ω上全純函式的研究,引出一類函式空間,即哈代空間 hp(p≥1)和與哈代空間h1有關的有界平均振幅空間(見BMO 空間)。
設Ω為n 維歐幾里得空間Rn的子域, 在 C(Ω)中取l(=1,2 ,…,∞) 階連續可微於Ω的函式 ƒ, 其全體記為Cl(Ω)。Cl(Ω) 中具緊支集的函式集合記為C
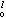 (Ω)。若Ω為Rn的子域閉包, 則ƒ 的條件改為對所有α=(α1,α2,…,αn)(其中 αi為非負整數,
(Ω)。若Ω為Rn的子域閉包, 則ƒ 的條件改為對所有α=(α1,α2,…,αn)(其中 αi為非負整數,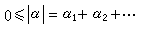
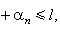 如l<∞;0≤|α|<∞,如l=∞),Dαƒ 有界且一致連續於IntΩ,得連續地開拓到嬠Ω,這樣的ƒ全體仍記為Cc(n)(Ω)。空間Cc(n)(Ω)的序列{ƒυ}在 Cc(n)(Ω)中收斂於0若且唯若對所有α ,0≤|α|≤l(0≤|α|< ∞,如l=∞),|Dαƒυ(x)|在Ω內任何緊集上一致收斂於0,序列{ƒυ}
如l<∞;0≤|α|<∞,如l=∞),Dαƒ 有界且一致連續於IntΩ,得連續地開拓到嬠Ω,這樣的ƒ全體仍記為Cc(n)(Ω)。空間Cc(n)(Ω)的序列{ƒυ}在 Cc(n)(Ω)中收斂於0若且唯若對所有α ,0≤|α|≤l(0≤|α|< ∞,如l=∞),|Dαƒυ(x)|在Ω內任何緊集上一致收斂於0,序列{ƒυ}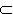 C
C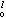 (Ω)在C
(Ω)在C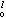 (Ω)中收斂於0。如果ƒυ的支集(v=1,2,…)含於Ω內與v無關的緊集中而{ƒυ}在Cc(n)(Ω)中收斂於0。
(Ω)中收斂於0。如果ƒυ的支集(v=1,2,…)含於Ω內與v無關的緊集中而{ƒυ}在Cc(n)(Ω)中收斂於0。 對域Ω嶅Rn,C∞(Ω)及 C悂(Ω)也分別記為E(Ω)及D(Ω)。它們是廣義函式論中的基本函式空間(見廣義函式)。對
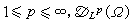 表 C∞(Ω)中使得對所有α , Dαƒ∈lp (Ω, m)(m 為勒貝格測度)的ƒ 全體,它是拓撲線性空間,零元的基本鄰域為
表 C∞(Ω)中使得對所有α , Dαƒ∈lp (Ω, m)(m 為勒貝格測度)的ƒ 全體,它是拓撲線性空間,零元的基本鄰域為 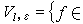
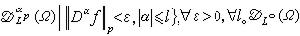 也記為B(Ω)(Ω=Rn時,Ω 得從記法中略去)。C∞中滿足急減條件
也記為B(Ω)(Ω=Rn時,Ω 得從記法中略去)。C∞中滿足急減條件 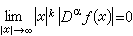
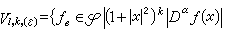
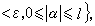
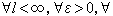
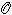 M ,
M ,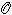 M中序列{ƒυ}收斂於零元指對每個α與每個φ∈φ,
M中序列{ƒυ}收斂於零元指對每個α與每個φ∈φ,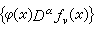 在Rn上一致收斂於0。
在Rn上一致收斂於0。 子域Ω嶅Rn上索伯列夫空間
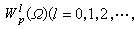
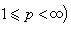
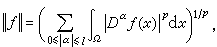
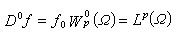 。 索伯列夫空間對研究偏微分方程問題解有重要意義且與其他函式空間概念有聯繫。
。 索伯列夫空間對研究偏微分方程問題解有重要意義且與其他函式空間概念有聯繫。 隨著不同函式空間的提出,常要了解對偶空間的組成和性質。從熟知的C(【0,1】)與有界線性泛函式的表達推廣得知:對緊空間Ω,C(Ω)的對偶空間同構於Ω中波萊爾集所成集合上定義的可列可加集函式 φ所組成的集合BV(Ω),它在以φ在Ω上的全變差為範數時為巴拿赫空間。對於
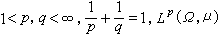 和lq(Ω,μ),lp和lq分別互為對偶空間。M(Ω,μ)的對偶空間同構於一賦范空間,它的元φ是定義在Ω中所有可測集上的有限可加集函式,絕對連續(即對於Ω上測度μ,μ(N)=0崊φ(N)=0)且在Ω上具有界變差,φ在 Ω上全變差為範數‖φ‖。l1(Ω,μ),l1,с的對偶空間分別同構於M(Ω,μ),m,l1。
和lq(Ω,μ),lp和lq分別互為對偶空間。M(Ω,μ)的對偶空間同構於一賦范空間,它的元φ是定義在Ω中所有可測集上的有限可加集函式,絕對連續(即對於Ω上測度μ,μ(N)=0崊φ(N)=0)且在Ω上具有界變差,φ在 Ω上全變差為範數‖φ‖。l1(Ω,μ),l1,с的對偶空間分別同構於M(Ω,μ),m,l1。 D、φ、E的對偶空間分別為D′、φ′、E′。因為D
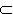 φ
φ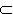 E、D′
E、D′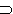 φ′
φ′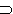 E′。D′的元稱為施瓦茲廣義函式。滿足條件
E′。D′的元稱為施瓦茲廣義函式。滿足條件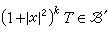 (對任何整數k>0)的廣義函式T稱為急減廣義函式,其全體記為
(對任何整數k>0)的廣義函式T稱為急減廣義函式,其全體記為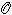 婞。從上面的規定及拓撲線性空間理論,有以下包含關係(1≤p<q<∞):
婞。從上面的規定及拓撲線性空間理論,有以下包含關係(1≤p<q<∞): 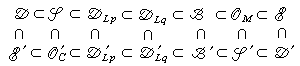
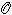 M ,
M ,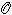 婞則上面包含關係對於以子域Ω嶅Rn取代Rn時仍成立。
婞則上面包含關係對於以子域Ω嶅Rn取代Rn時仍成立。 兩線性空間A,B間包含關係,用記法A嶅B,在集合及代數結構意義上理解。有時兩線性拓撲空間A,B間包含關係A嶅B同時還表示映射A→B是連續的,這時A嶅B表A單射入B。在函式空間,廣義函式的空間,索伯列夫空間方面有許多這類關係,最常見的如lp(Ω,μ)嶅lq(Ω,μ),q<p。