對偶性
觀察映射
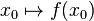 泛函式
泛函式是一個函式,在這裡,x0是函式f的自變數。
同時,將函式映射至一個點的函式值
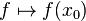 泛函式
泛函式是一個泛函,在此是一個參數
只要是一個從向量空間至一個布於實數的體的線性轉換,上述的線性映射彼此對偶,那么在泛函分析上,這兩者都稱作線性泛函。
相關說明
擬賦范空間、局部凸拓撲線性空間、賦范空間等的表征主要在於分別在各空間上定義的次加性泛函式,即擬範數、半範數族、範數等。測度空間中的測度,即對應於某種集合的值也可理解為泛函式。對於給定函式的不定積分也可類似地看待。
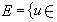
通常的函式在 或C(是自然數)中的集合上定義。泛函式常在函式空間甚至抽象空間中的集合上定義,對集合中每個元素取對應值(實數或複數)。通俗地說,泛函式是以函式作為變元的函式。泛函式概念的產生與變分學問題的研究發展有密切關係。 傳統上,泛函通常是指一種定義域為函式,而值域為實數的“函式”。換句話說,就是從函式組成的一個向量空間到實數的一個映射。也就是說它的輸入為函式,而輸出為實數。泛函的套用可以追溯到變分法,那裡通常需要尋找一個函式用來最小化某個特定泛函。在物理學上,尋找某個能量泛函的最小系統狀態是泛函的一個重要套用。
觀察映射
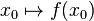 泛函式
泛函式是一個函式,在這裡,x0是函式f的自變數。
同時,將函式映射至一個點的函式值
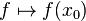 泛函式
泛函式是一個泛函,在此是一個參數
只要是一個從向量空間至一個布於實數的體的線性轉換,上述的線性映射彼此對偶,那么在泛函分析上,這兩者都稱作線性泛函。
擬賦范空間、局部凸拓撲線性空間、賦范空間等的表征主要在於分別在各空間上定義的次加性泛函式,即擬範數、半範數族、範數等。測度空間中的測度,即對應於某種集合的值也可理解為泛函式。對於給定函式的不定積分也可類似地看待。
出 版 開
基本信息 內容介紹§1.1 §1.3 §2.1
基本相信 內容簡介 目錄 前言廣義函式,數學概念,是古典函式概念的推廣。關於廣義函式的研究構成了泛函分析中有著廣泛套用的一個重要分支。廣義函式被廣泛地套用於數學、物理、力學以及分析數...
來歷 爭論 引進 重要影響 三大分類《實變函式與泛函分析概要(第1冊)(第4版)》是高等教育出版社出版的圖書。本書可作為綜合大學、理工大學、師範院校數學類專業的教學用書,也可作為有關研究生...
內容簡介 目錄《實變函式與泛函分析 》是 高等教育出版社 出版的圖書,這次修訂繼續保持簡明易學的風格,力圖擺脫純形式推演的論述方式,著重介紹實變函式與泛函分析的基本思...
基本信息 內容簡介內容介紹《近代實變函式論與泛函式分析》由東北大學出版社出版,內容包括:實變函式論、集和點集、開集、閉集與完全集、測度、可測函式與積分、度量空間、線性運算元...
內容介紹版 次:1 本:32開
基本信息 內容介紹2.集合的運算 4.可數集合 5.不可數集合
圖書信息 內容簡介 目錄