基本介紹
李普希茨是德國數學家、物理學家。主要研究數學分析、數論、微分方程、多維幾何、力學和物理。1859年,他發表了關於藉助線積分給出貝塞爾函式的漸近展開式的嚴格研究。1864年,在研究傅立葉級數收斂性時,給出了以他的姓命名的充分條件。1876年,他改進了柯西關於常微分方程存在定理的條件。現在這一條件就被稱為 李普希茨條件。他對n維空間的子空間給出了一些新的結果。他還是微分不變數研究的創始人之一,在其工作中已出現了共變微分這種運算 。
R.(O.S.)李普希茨(1832-1903年)的數學研究涉及數論、貝塞爾函式論、傅立葉級數論、常微分方程、分析力學、位勢理論及黎曼微分幾何,其中在微分方程和微分幾何方面尤為突出。1873年他對A.-L.柯西提出的微分方程初值問題解的存在惟一性定理作出改進,提出著名的“李普希茨條件”。存在性定理的證明有力地推進了對微分方程定性理論以及解的近似計算的研究。
李普希茨被認為是(G.F.)B.黎曼事業的繼承者之一。黎曼於1854年系統地闡述了高維流形微分幾何的主要內容,並於1868年發表了研究n維流形的度量結構的文章。1869年起李普希茨對黎曼的思想作出進一步闡述和推廣,其中對n維黎曼流形的子流形性質以及對微分不變數的研究,取得了開創性的成果。他還是最早使用共變微分研究微分不變數的人,這個概念後來被G.里奇有效地用於張亮分析 。
李普希茨條件
概念介紹
 李普希茨
李普希茨 李普希茨
李普希茨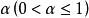 李普希茨
李普希茨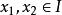 李普希茨
李普希茨李普希茨條件(Lipschitz condition)亦稱赫爾德條件,是限制函式增量變化大小的一種不等式形式的條件。若 是區間 上的函式,存在正的常數L和 ,使得只要 ,就有
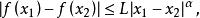 李普希茨
李普希茨 李普希茨
李普希茨 李普希茨
李普希茨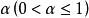 李普希茨
李普希茨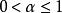 李普希茨
李普希茨則函式 稱為在區間 上滿足 α階李普希茨條件,或稱為I上的α階李普希茨函式,記為f∈Lipα(I)或f∈Λ(I)。對任意 ,α階李普希茨函式都是連續函式。特別地,屬於Lip1的函式為絕對連續函式,因而除去一個勒貝格零測度集之外處處可微。一階李普希茨條件是李普希茨(Lipschitz,R.(O.S.))於1864年研究傅立葉級數的收斂判別法時引進的.不少作者把一階李普希茨條件稱為李普希茨條件。1876年,他把它用於微分方程有惟一解問題的討論。的α階李普希茨條件其實是赫爾德引進的,所以又稱為α階赫爾德條件。
相關分析
 李普希茨
李普希茨 李普希茨
李普希茨1.設 為一函式,k為一正常數,若對於點 之鄰域中的所有點x,都有
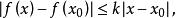 李普希茨
李普希茨 李普希茨
李普希茨 李普希茨
李普希茨則稱 在點滿足李普希茨條件。
 李普希茨
李普希茨 李普希茨
李普希茨 李普希茨
李普希茨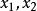 李普希茨
李普希茨2.設 為定義在 上的函式,k為一正常數, 若對於中任意兩點,都有
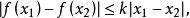 李普希茨
李普希茨 李普希茨
李普希茨 李普希茨
李普希茨則稱在區間上滿足李普希茨條件。
 李普希茨
李普希茨 李普希茨
李普希茨 李普希茨
李普希茨若函式在上滿足李普希茨條件,則該函式在上必為絕對連續函式。換言之,絕對連續為李普希茨條件之必要條件,而李普希茨條件為絕對連續之充分條件。
 李普希茨
李普希茨 李普希茨
李普希茨 李普希茨
李普希茨若函式在上之任一點均有連續導數, 則該函式在上必滿足李普希茨條件。換言之, 有連續導數是李普希茨條件之充分條件,而滿足李普希茨條件是有連續導數之必要條件。
 李普希茨
李普希茨 李普希茨
李普希茨3.設為一函式,k為一正常數,若對於點鄰域中之所有點x,都有
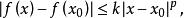 李普希茨
李普希茨 李普希茨
李普希茨 李普希茨
李普希茨則稱在點滿足 p次李普希茨條件。
 李普希茨
李普希茨 李普希茨
李普希茨 李普希茨
李普希茨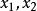 李普希茨
李普希茨4.設為定義在上的函式,k為一正常數, 若對於上之任意兩點,都有
 李普希茨
李普希茨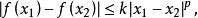 李普希茨
李普希茨則稱該函式在上滿足p次李普希茨條件。
顯然,1,2分別是3,4當p=1時之特例。


