余集[數學定義]

補集一般指絕對補集，即一般地，設是一個集合，是的一個子集，由中所有不屬於的元素組成的集合，叫做子集在中的絕對補集。在集合論和數學的其他分支中，存在補集的兩種定義：相對補集和絕對補集。

基本信息

• 中文名：余集
• 籍貫：浙江
• 出生地：仁和

定義

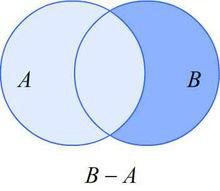相對補集（差集）示意圖

在集合論和數學的其他分支中，存在補集的兩種定義：相對補集和絕對補集。

1、相對補集

若 A和 B 是集合，則 A 在 B 中的相對補集是這樣一個集合：其元素屬於 B但不屬於 A， B - A = { x| x∈B且x∉A}。

2、 絕對補集

若給定全集 U，有 A⊆U，則 A在 U中的 相對補集稱為 A的 絕對補集（或簡稱 補集），寫作∁A。

注意：學習 補 集的概念，首先要理解全集的相對性，補集符號∁A有三層含義：

1、A是U的一個子集，即A⊆U；

2、∁A表示一個集合，且∁A⊊U；

3、∁A是由U中所有不屬於A的元素組成的集合，∁A與A沒有公共元素，U中的元素分布在這兩個集合中。

全集與補集

全集是一個相對的概念，只包含所研究問題中所涉及的所有元素， 補集只相對於相應的全集而言。如：我們在整數範圍內研究問題，則 Z為全集，而當問題拓展到實數集時，則 R為全集，補集也只是相對於此而言。

相關運算

補律與差集

•根據補集的定義，∁A={x|x∈U且x∉A}，B-A={x|x∈B且x∉A}

•A∩∁A=∅

•A∪∁A=U

De Morgan定律

摩根定律，又叫反演律，用文字語言可以簡單的敘述為：兩個集合的交集的補集等於它們各自補集的並集，兩個集合的並集的補集等於它們各自補集的交集。

若集合A、B是全集U的兩個子集，則以下關係恆成立：

（1）∁（A∩B）=（∁A）∪（∁B），即“交之補”等於“補之並”；

（2）∁（A∪B）=（∁A）∩（∁B），即“並之補”等於“補之交”。