定理內容
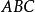西姆森定理
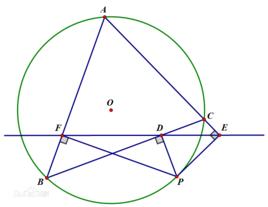
西姆森定理 西姆森定理 西姆森定理 西姆森定理西姆松定理說明：有三角形 ，平面上有一點 。 在三角形三邊上的投影（即由 到邊上的垂足）共線（此線稱為 西姆松線或譯 西摩松線, Simson line）若且唯若 在三角形的外接圓上 。
圖1.西姆森定理說明圖相關的結果有：
西姆森定理
西姆森定理 西姆森定理（1）稱三角形的垂心為 。西姆松線和 的交點為線段 的中點，且這點在九點圓上。
（2）兩點的西姆松線的交角等於該兩點的圓周角。
西姆森定理 西姆森定理（3）若兩個三角形的外接圓相同，這外接圓上的一點 對應兩者的西姆松線的交角，跟 的位置無關。
證明
如圖1，若L、M、N三點共線，連結BP，CP，則因PL垂直於BC，PM垂直於AC，PN垂直於AB，有B、P、L、N和M、P、L、C分別四點共圓，有∠PBN = ∠PLN = ∠PLM = ∠PCM，故A、B、P、C四點共圓。
若A、B、P、C四點共圓，則∠PBN = ∠PCM。因PL垂直於BC，PM垂直於AC，PN垂直於AB，有B、P、L、N和M、P、L、C四點共圓，有∠PLN = ∠PBN = ∠PCM =∠PLM，故L、M、N三點共線。
