套用定理
△ ABC的外接圓上的一點 D的關於邊 BC、 CA、 AB的對稱點和△ ABC的垂心 H同在一條(與西姆松線平行的)直線上。這條直線被叫做點 D關於△ ABC的鏡象線.
定理證明
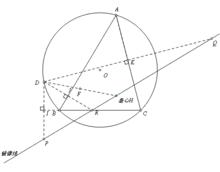 史坦納定理
史坦納定理相比直接證明史坦納定理,證明史坦納定理的套用定理更為簡便!
如圖,設點 D關於邊 BC、 CA、 AB的對稱點分別為 P、 Q、 R,則有:
∠ BPC=∠ BDC=∠ BAC=180°-∠ BHC(垂心的性質)
所以 H、 B、 C、 P四點共圓,同理有:
所以 H、 C、 A、 Q四點共圓.
所以 H、 A、 B、 R四點共圓.
證明垂心 H在 PQ上只要證明∠ CHP與∠ CHQ互補或相等.
由四點共圓和對稱性
∠ CHP=∠ CBP=∠ CBD
∠ CHQ=∠ CAQ=∠ CAD
∠ CBD與∠ CAD互補
所以有∠ CHP與∠ CHQ互補,即 H在 PQ上.
史坦納定理的套用定理證畢,顯然西姆松線是三角形 DPQ的中位線,所以 DH與西姆松線的交點一定是 DH的中點,史坦納定理得證.
定理推論
在一個圓周上有4點,以其中任三點作三角形,再作其餘一點的關於該三角形的西姆松線,這些西姆松線交於一點。
