正文
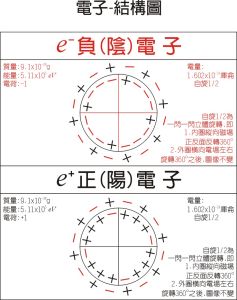 電子-模型圖
電子-模型圖 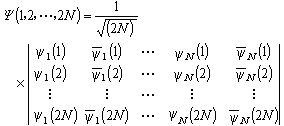 (1)
(1)
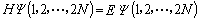 (2)
(2)
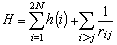 (3)
(3)
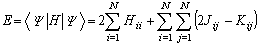 (4)
(4)
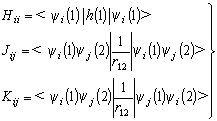 (5)
(5)
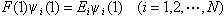 (6)
(6)
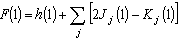 (7)
(7)
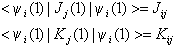
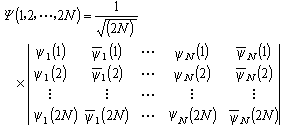
利用自洽疊代過程處理分子軌道的方法。分子軌道法認為在分子中存在著一系列單電子空間波函式,稱為分子軌道,每一個分子軌道都有確定的能量與之對應,而整個分子的波函式,可以近似地用分子軌道的乘積來描述。按照泡利原理,總波函式必須是反對稱的,即交換任何兩個電子的坐標後,波函式將只改變一個符號,斯萊特行列式波函式滿足這個要求。
 電子-模型圖
電子-模型圖 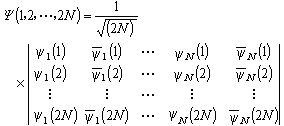 (1)
(1)
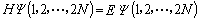 (2)
(2)
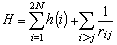 (3)
(3)
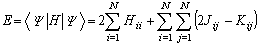 (4)
(4)
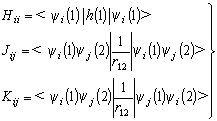 (5)
(5)
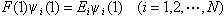 (6)
(6)
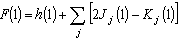 (7)
(7)
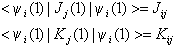
分子軌道理論又稱分子軌道法(Molecular Orbital Theory)或MO法,1932年由美國化學家馬利肯(R.S.Mulliken)及德國物...
分子軌道的歷史 理論簡介 軌道簡介 線性組合原則 軌道能量特里方程。使用自洽場疊代方式求解這個方程(見自洽場分子軌道法),就可得到...其他學科的滲透。計算方法主要分為:①分子軌道法(簡稱MO法,見分子軌道理論);②價鍵法(簡稱VB法,見價鍵理論)。以下只介紹分子軌道法,它是...
簡介 發展 計算方法 套用範圍 量子化學大家這個方程(見自洽場分子軌道法),就可得到體系的電子結構和性質。哈特里方程...分類主要分為:①分子軌道法(簡稱MO法,見分子軌道理論);②價鍵法(簡稱VB法,見價鍵理論)。以下只介紹分子軌道法,它是原子軌道對分子的推廣...
分類 RHF 方程 UHF 方程 從頭計算法Fock自洽場方法84 自洽場方法84 Feynman定理85...原子分子97 雜化軌道97 2分子軌道法處理水分子99 硼烷...197 5部分CI197 多組態自洽場199 多組態自洽場...
算法或自洽場半經驗法計算鍵長。 鍵角定義鍵角是指在分子中,一個原子與其他...的H-Cl鍵就是極性共價鍵。鍵級鍵級又稱鍵序,是分子軌道法中表示相鄰...離解能定義298.15k,將1mol氣態雙分子AB的化學鍵斷開成為氣態...
鍵參數的定義 鍵能 鍵長 鍵角 其他參數出了各種半經驗的近似計算方法,主要是自洽場分子軌道法和60年代開始發展...定量的自洽場近似方法,例如由J.A.波普爾引入的全略微分重疊法、間略微分...、E.休克爾的分子軌道理論及雜化軌道理論等,推動了有機化學的發展,這是...
理論有機化學 配圖 相關連線,α作為參數由實驗值確定。 在自洽場(SCF)分子軌道法中,庫侖積分Jij..., 必須注意區分。 在原子的自洽場計算中, 反映處在兩個原子軌道上的兩個電子..., 產生多種相互作用, 又由於可採用價鍵法和分子軌道法等不同方法, 所以...
——“自洽場過程的數學方法”組成。實驗部分含10個獨立的計算設計,從基本的分子...(AB INITIO)方法第二章 半經驗分子軌道法第三章 包含電子相關... SPARTAN使用簡介參考文獻附錄 自洽場過程的數學方法參考文獻 ...
內容簡介 目錄