原子的量子理論
正文
以量子力學為基礎的關於原子結構的理論。N.玻爾關於原子結構的理論(見玻爾氫原子理論是原子的量子理論的先驅,它的建立推動了原子結構的研究。研究的深入又揭示了玻爾理論與實驗結果間的一系列矛盾。而解決這些矛盾則導致量子力學的誕生。氫原子是最簡單的原子,只有一個電子繞質子運動。用量子力學處理氫原子得到的結果精確度最高,處理多電子原子問題困難則大得多,但氫原子理論中的一些結果對認識多電子原子的運動很有幫助。下面介紹氫原子的量子力學理論的概要,再略述多電子原子的量子力學理論。
氫原子 氫原子核的質量約為電子質量的1836倍,故可把運動簡化為電子在靜止的原子核的庫侖場中運動,以r代表電子到核的距離,-e代表電子的電荷,則電子的位能為
 。根據量子力學的理論,電子的運動狀態用一波函式 Ψ來描寫。波函式 Ψ是電子坐標 r的函式。
。根據量子力學的理論,電子的運動狀態用一波函式 Ψ來描寫。波函式 Ψ是電子坐標 r的函式。 表示電子在空間各點出現的幾率密度。當電子與氫原子核組成原子時,電子受庫侖力的作用被束縛在核附近一小區域內。與此相應,幾率密度
表示電子在空間各點出現的幾率密度。當電子與氫原子核組成原子時,電子受庫侖力的作用被束縛在核附近一小區域內。與此相應,幾率密度 將只在核附近的一個小區域內不等於零,這種狀態叫束縛態。
將只在核附近的一個小區域內不等於零,這種狀態叫束縛態。 要確定束縛態波函式,需要解定態薛丁格方程
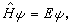 (1)
(1)
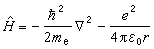 。 (2)
。 (2)
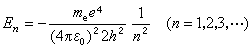 , (3)
, (3)
當電子在庫侖場中運動時,能量與軌道角動量都是守恆量。用量子力學的語言,即電子的能量E、軌道角動量z分量Lz(有時用
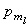 表示)與
表示)與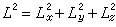 可以同時有確定值。此時波函式ψ除需滿足式(1)還應同時滿足本徵方程
可以同時有確定值。此時波函式ψ除需滿足式(1)還應同時滿足本徵方程 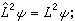 (4)
(4)
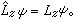 (5)
(5)
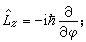 (6)
(6)
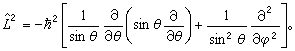 (7)
(7)
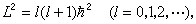 (8)
(8)
解式(5)得Lz的值為
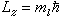 , (9)
, (9)
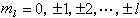 。 (10)
。 (10)
當電子波函式ψ同時滿足式(1)、(4)、(5)時,它描寫電子的E、L2、Lz同時有確定值的狀態。此時波函式用r、θ、嗞作為變數,並用量子數n、Л、ml作為標記。則有
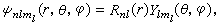 (11)
(11)
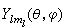 是球諧函式,Rnl(r)叫做徑向波函式。
是球諧函式,Rnl(r)叫做徑向波函式。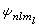 即表示電子能量等於
即表示電子能量等於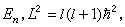
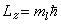 的狀態。
的狀態。 式(10)表明磁量子數ml受角量子數l的限制。角量子數Л則受主量子數n的限制,關係是
Л=n-1,n-2,…,1,0。 (12)
由n、l、ml間的關係可見,對應於一個能級En有n2個獨立的波函式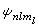 ,它們分別描寫不同角動量的態。
,它們分別描寫不同角動量的態。  原子的量子理論
原子的量子理論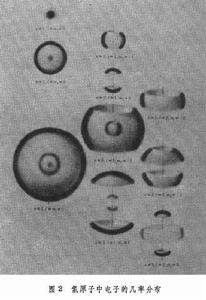 原子的量子理論
原子的量子理論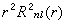 。由圖可見,幾率密度具有束縛態的特徵。圖中虛線表示
。由圖可見,幾率密度具有束縛態的特徵。圖中虛線表示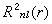 與r的關係,實線表示
與r的關係,實線表示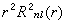 與r的關係。
與r的關係。 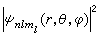 給出了氫原子中電子在各點出現的幾率。圖2給出了n、Л、ml不同時電子的幾率分布。在l=0時,幾率分布是球對稱的。在l厵0時,幾率分布對於z軸是對稱的。圖2中,z軸是垂直的,並通過幾率分布的對稱中心(即原子核)。
給出了氫原子中電子在各點出現的幾率。圖2給出了n、Л、ml不同時電子的幾率分布。在l=0時,幾率分布是球對稱的。在l厵0時,幾率分布對於z軸是對稱的。圖2中,z軸是垂直的,並通過幾率分布的對稱中心(即原子核)。 考慮到電子具有自鏇以後,波函式還須擴充到能描寫電子自鏇狀態。已知自鏇角動量的 z分量sr(有時用pms表示)也是量子化的,即
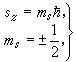 (13)
(13)
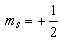 與
與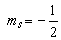 的狀態。於是包括自鏇狀態的波函式用四個量子數n、l、ml、ms作為標記,則波函式為
的狀態。於是包括自鏇狀態的波函式用四個量子數n、l、ml、ms作為標記,則波函式為 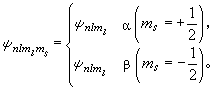 (14)
(14)
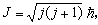 (15)
(15)
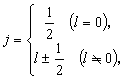 (16)
(16)
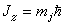 。 (17)
。 (17)
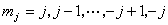 。 (18)
。 (18)
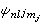 , 它的數學表示式與
, 它的數學表示式與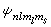 不同的。在不考慮自鏇軌道耦合時,
不同的。在不考慮自鏇軌道耦合時,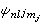 與
與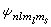 都代表相同的能量狀態。在考慮了自鏇軌道耦合以後,電子狀態用
都代表相同的能量狀態。在考慮了自鏇軌道耦合以後,電子狀態用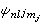 描寫更為確切。
描寫更為確切。 由於電子在氫原子中運動速度v與光速с的比值約為10-3的數量級。 比較精細的理論必須考慮電子質量隨速度改變的相對論效應。P.A.M.狄喇克提出了一個考慮了電子自鏇的相對論運動方程。在狄喇克的理論中,波函式具有四分量。寫成數學形式,即
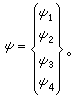 (19)
(19)
根據狄喇克理論,氫原子能級公式為
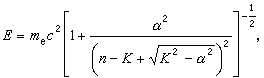 (20)
(20)
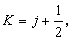 α為精細結構常數,它的表示式與數值為
α為精細結構常數,它的表示式與數值為 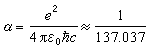 。 (21)
。 (21)
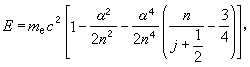 (22)
(22)
根據狄喇克理論,電子狀態仍可用量子數n與j描述,能級值也決定於量子數n與j,這樣,當兩個狀態具有相同n與j但l不同時,能量應該相同。例如,2s2S½與2p2P½能級應該相同。1947年W.E.蘭姆與R.C.雷瑟福發現此二能級有微小差異,人們稱此差異為蘭姆移位。套用量子電動力學的理論可以解釋。
多電子原子 從氦元素開始,原子至少有二個電子,屬於多電子原子。如果原子序數為Z,則有Z個電子。即使不考慮原子核的運動,仍應考慮Z個電子的運動,因一個電子的運動要用三個空間坐標(x,y,z)與一個自鏇坐標sr描寫,Z個電子的運動就要用4Z個坐標描寫。引入縮寫
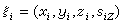 (23)
(23)
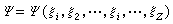 (24)
(24)
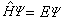 (25)
(25)
多電子原子的哈密頓算符要比氫原子的複雜得多。哈密頓算符彑主要包括每個電子的動能算符,每個電子在原子核場中的位能,以及電子間的相互作用。正是電子間的相互作用使問題複雜化。這時,每一電子的運動受到其他電子運動的影響,這使式(25)不存在嚴格的解。
在處理多電子問題時,常引入一合理的物理模型,即獨立粒子模型。在此中假設每一電子運動仍可用單粒子波函式
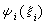 來描寫。這裡
來描寫。這裡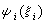 表示第 i個電子在原子核以及其他電子場中運動的波函式。考慮到每一電子在核周圍迅速運動,電子場可以用平均場代替,這平均場又可用一中心場來近似表示。於是問題簡化為研究每一電子在中心場中的運動。
表示第 i個電子在原子核以及其他電子場中運動的波函式。考慮到每一電子在核周圍迅速運動,電子場可以用平均場代替,這平均場又可用一中心場來近似表示。於是問題簡化為研究每一電子在中心場中的運動。 當電子在中心場中運動時,如同氫原子一樣,電子的能量、軌道角動量與自鏇可以同時有確定值。電子狀態仍然可以用量子數n、l、ml、ms表示。單電子波函式仍可記作
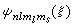 。它的具體數學表示式則不同於氫原子的波函式。在考慮了自鏇軌道耦合以後,電子狀態也可以用量子數n、l、j、mj表示。總之在獨立粒子模型中,每一電子狀態可用四個量子數以及相應波函式表示。
。它的具體數學表示式則不同於氫原子的波函式。在考慮了自鏇軌道耦合以後,電子狀態也可以用量子數n、l、j、mj表示。總之在獨立粒子模型中,每一電子狀態可用四個量子數以及相應波函式表示。 計算得單電子波函式以後,可以得到系統的波函式。最初在D.R.哈特里提出的理論中
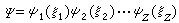 , (26)
, (26)
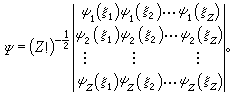 (27)
(27)
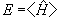 (28)
(28)
多電子原子的核心問題是求出單電子波函式
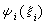 。根據物理模型,每一電子是在其他電子平均場中運動,而平均場又要通過單電子波函式來計算。這種方法叫量子力學的自洽場近似法。自洽場法中要求解一組微分積分方程以得到單電子波函式。哈特里最初從式(26)出發建立了一組方程,叫哈特里方程。以後B.A.福克考慮到正確的波函式應該用式(27)表示,得到了更精確的方程,叫哈特里—福克方程。求單電子波函式的另一種方法是用量子力學的變分法。此法在研究輕元素時用得更多些。無論哪一種方法都必須進行數值計算。計算工作量很大,要用大型電子計算機。
。根據物理模型,每一電子是在其他電子平均場中運動,而平均場又要通過單電子波函式來計算。這種方法叫量子力學的自洽場近似法。自洽場法中要求解一組微分積分方程以得到單電子波函式。哈特里最初從式(26)出發建立了一組方程,叫哈特里方程。以後B.A.福克考慮到正確的波函式應該用式(27)表示,得到了更精確的方程,叫哈特里—福克方程。求單電子波函式的另一種方法是用量子力學的變分法。此法在研究輕元素時用得更多些。無論哪一種方法都必須進行數值計算。計算工作量很大,要用大型電子計算機。 參考書目
周世勛編:《量子力學教程》,人民教育出版社,北京,1979。
G.Herzberg,Atomic Spectra and Atomic Structure,Dover,New York,1944.
J.C.Slater, Quantum Theory of Atomic Structure,Vol.1,2,McGraw-Hill,New York,1960.