正文
電子-模型圖一種化學鍵理論，是原子軌道理論對分子的自然推廣。其基本觀點是:物理上存在單個電子的自身行為,只受分子中的原子核和其他電子平均場的作用，以及泡利不相容原理的制約；數學上則企圖將難解的多電子運動方程簡化為單電子方程處理。因此，分子軌道理論是一種以單電子近似為基礎的化學鍵理論。描寫單電子行為的波函式稱軌道（或軌函），所對應的單電子能量稱能級。對於任何分子，如果求得了它的系列分子軌道和能級，就可以像討論原子結構那樣討論分子結構，並聯繫到分子性質的系統解釋。有時，即便根據用粗糙的計算方案所得到的部分近似分子軌道和能級，也能分析出很有用處的定性結果。
分子軌道理論
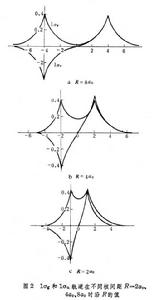分子軌道理論氫分子離子的分子軌道 正如在原子軌道理論中，氫原子的嚴格解提供了進一步發展的理論模式，氫分子離子H娚中,單個電子在固定核間距
的雙質子場中的波動方程解，是分子軌道理論進程中的基石。H娚的分子軌道用符號σ、π、
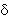分子軌道理論、…表征,對應於精確解中的量子數
＝0,±1,±2,…,它描述相對於核間距
的軌道對稱行為。此外，還需用g和u表征相對於分子中心反演的對稱行為。綜合起來,H娚的分子軌道用σ
、σ
、π
、π
、…等符號表征，藉助精確求解固定核間距
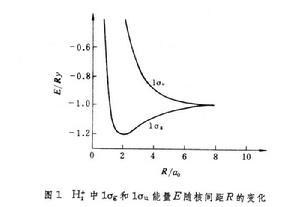
的波動方程獲得。圖1給出兩個最低軌道1σ
和1σ
的能量
隨
的變化曲線。1σ
能級有一極小值－1.20
(里德伯能量),出現在
＝2
處(
為玻爾半徑,圖2）,代表基態；當
增大以至無窮時, 1σ
能量趨近-1.0
。兩者差值0.20
就是H娚的離解能。1σ
的行為不同, 能量隨
減小而單調上升,顯示排斥態的本質。1σ
和1σ
也被稱作成鍵軌道和反鍵軌道。1σ
均取正值，1σ
則在中心兩端發生符號變化,但極值均出現在質子所在處，且伴隨
變小；1σ
在核間區數值增大，描寫了電子在分子中的轉移。隨著
的增大,1σ
和1σ
的函式值漸近於式(1)～(2)：
(1)
(2)
式中
和
是歸一化係數;
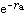分子軌道理論和
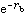分子軌道理論
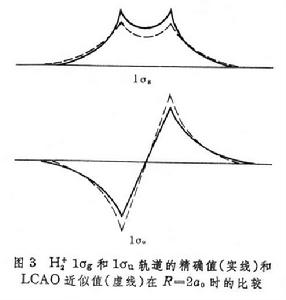分子軌道理論分別是兩個組成氫原子上的 1s原子軌道。圖3 給出
＝2
時，1σ
和1σ
軌道的精確值和按式(1)與(2)的近似值的比較,說明式(1)與(2)的近似程度是很好的。式(1)和(2)表示，分子軌道可以近似地當作原子軌道的線性組合,簡寫為LCAO（見量子化學計算方法）。當
很大時，結果是準確的，即使
達到分子核間距大小時,也給出不錯的結果。這一點啟發了對複雜分子也可採用LCAO方法去尋找近似分子軌道。這是因為在分子中，靠近一個核的電子主要受到該核的勢場的作用；而受到其餘核的聯合作用，則小得多，因此在近核處，分子軌道必定近似於該核的原子軌道。對於整個空間的任何一點，可以構想分子軌道由有關的原子軌道線性組合而成。一般的形式是：
(3)
式中ψ 代表分子軌道或軌函；
是屬於各組成原子的原子軌道；
是待定係數,由變分法確定。還應指出,LCAO是一種可行的近似方式，但不是唯一的近似方式。
任意雙原子分子的分子軌道用原子軌道線性組合法LCAO近似來討論任意雙原子分子中，分屬兩個原子的一對原子軌道形成分子軌道的最優條件。這時,式(3)採取以下簡單形式：
ψ＝cφ＋cφ (4)
代入波動方程
ψ＝
ψ，得到近似能級
：
(5)
式中
和
分別是原子軌道
和
的庫侖積分，可看作
和
的能量,即
＝
，
＝
；
＝
稱共振積分,與
和
的重疊情況有關,一般取負值,
稱重疊積分，可當作零處理,而不影響定性結論。最優條件由
取極值確定，即：
(6)
上式給出一組
、
的齊次方程組，由係數組成的久期方程（見休克爾分子軌道法）得到：
(7)
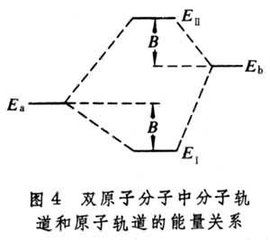
設
＜
，則式(7)的含意可用圖4 表示。
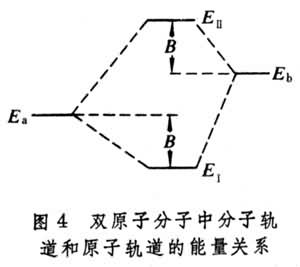分子軌道理論由此看出，有效的成鍵作用決定於
值的大小,後者又與原子軌道能量差|
-
|以及重疊情況
有關,從而可歸納為三個條件：
① 能量近似條件:指|
-
|越小越好,當|
-
|＝0時，
最大，等於|
|。
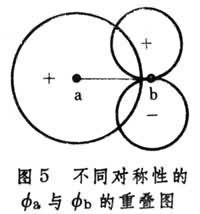
② 最大重疊條件：
與
的重疊越大(圖5
),
的絕對值也可能越大。
分子軌道理論③ 對稱性條件：有時
與
雖然重疊,但
＝0,例如當核間距
選作
軸（表1），
＝s，
＝p
，這是因為s軌道相對
平面為對稱的，而p
為反對稱的。
分子軌道理論將式(7)用於同核雙原子分子，
和
可以是分屬兩原子的同一原子軌道，這時有：
(8)
ψ
對分子中心為對稱,屬於g；ψ
為反對稱,屬於u。其次，若
＝
＝s(或＝p
),ψ
和ψ
均對核間距(
軸)為軸對稱，屬於
＝0的σ態；但對
＝
＝p
(或p
)，則存在通過
的節面，屬於
＝±1的π態,細節列於表2中。
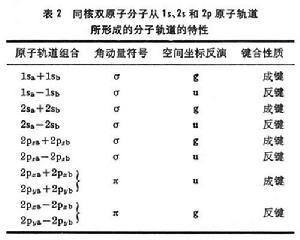分子軌道理論分子軌道的能量決定於組成原子軌道的類型和原子軌道間的重疊，例如σ
1s和σ
1s比σ
2s低得多,這是由於原子軌道1s的能量比2s的低得多。同理，因為除氫原子外，2s能量顯著低於2p的能量，故σ
2s比σ
2p能量低。另外,只要核間距不很小，兩個2s軌道或兩個2p
軌道之間的重疊比兩個2p
或2p
之間的重疊大得多，因此成鍵和反鍵π軌道間的能量差比對應的σ軌道的差小。根據這種論述,表2中所列分子軌道次序可預料為：
σ1s＜σ1s＜σ2s＜σ2s＜σ2p
＜π2p＜π2p＜σ2p (9)
上式是一種最粗糙的軌道近似，更好的近似是包含更多的原子軌道，這些原子軌道符合有效成鍵作用的三條件。例如，代替單純的2s以及2p的LCAO所形成的σ型分子軌道應為：
(10)
、
、
、
確定後的四個σ軌道比原來的σ
2s、σ
2s、σ
2p和σ
2p更接近實際，其中σ
2s、σ
2s將降低,σ
2p及σ
2p則升高。加上當核間距變小時，π
2p要降低,導致式(9)中，σ
2p與π
2p次序的可能顛倒：
π2p＜σ2p (11)
N
分子就屬於這一類型。
有了式(9)與(10)的能級次序,就可按能量最低原理和泡利原理來預言同核雙原子分子的基態（表3）。
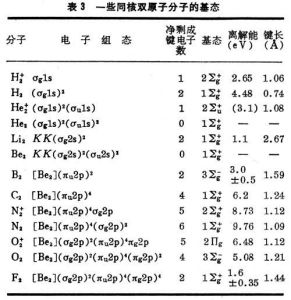分子軌道理論表中的符號Σ、Π、… 意義與σ、π、… 相同，具有沿核間距方向角動量的含義,標誌完整分子的態,由各個單電子軌道確定；右上角的＋、－號指對平分兩核的鏡面反映為對稱或反對稱而言。
多原子分子的分子軌道 以上基於單電子波動方程近似解的軌道概念和方法，可自然地向複雜的多原子分子推廣。對雙原子分子，存在沿核間距方向的角動量量子數
＝0,±1,…等來表征軌道或態；但對多原子分子，找不到象H娚那樣簡單而典型的分子，不能精確求解，給問題的討論造成了麻煩。但由於弄清了量子數所表征的分子軌道對稱性本質來源於分子自身的對稱性，因而對稱性分析（群論）會給出任何分子電子狀態的重要信息，而無需知道分子軌道的具體函式。這方面的進展是巨大的，例如群論在化學中的套用，能級相關圖、分子軌道對稱守恆原理等的評述。此外，建立在單電子能級和軌道近似基礎上的理論計算方法已發展起來，如自由電子分子軌道法、休克爾分子軌道法及推廣的休克爾分子軌道法等。
如前所述，分子軌道和能級是單電子波動方程的本徵解，即滿足：
Hψ＝εψ (12)
式中
是單電子哈密頓算符,其中的位能描寫一個電子在固定分子骨架及其餘電子的平均作用。因而,
與其餘電子的運動狀態,即軌道有關。前面的討論絲毫未觸及
的具體形式，也未對分子軌道作過嚴格定義，所得結論是定性地適用的。為適應理論的定量化發展，已經推導出著名的哈特里-福克方程（見自洽場分子軌道法）,對於閉殼層電子體系，式(12)中的
採取福克算符的形式：
(13)
式中
是純核場中單個電子的哈密頓算符，2
-
＝
和2
(
≠
)代表其餘電子的平均靜電勢，
(
≠
)稱交換勢能，它來源於泡利不相容原理導致自鏇相同電子間的相關作用。
和
的表示式均明顯地與分子軌道有關，例如：
(14)
式中(1)代表所考慮的單電子的坐標;(2)為另一電子,其分子軌道為ψ
(2)；
代表兩電子間距離。因此,式(12)的求解需事先構想一組ψ
，按式(13) 求出
，然後得到一組新的ψ
，重複這種步驟，直到最後一次循環中, 試探的ψ
與解出的ψ
接近和相同為止，稱為自洽。
採用LCAO方法，分子軌道ψ
按式(3)表示成原子軌道
(
＝1,2,…,
)的線性組合：
(15)
代入(12)式,左右兩端乘以
奰並積分，得到一組
的方程組：
(16)
式中
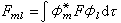分子軌道理論；
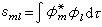分子軌道理論。求解歸結為久期方程的本徵值
和本徵向量
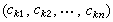分子軌道理論的自洽計算：
哈特里－福克方程雖然較仔細地考慮了電子間的排斥作用，但由於平均勢場模型仍然使一部分固有的“相關作用”未予考慮，因而理論計算結果仍未達到定量符合實驗值的精度。改進的途徑是考慮組態相互作用，已經出現了多種組態相互作用分子軌道從頭計算程式，用於量子化學研究。
參考書目
R.Dandel, G.Leroy, D.Peters and M.Sana,
,John Wiley & Sons, New York, 1983.
