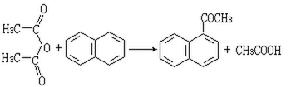
量子化學計算方法
正文
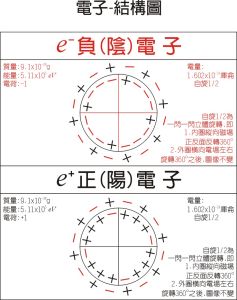
簡史 分子軌道法的核心是哈特里-福克-羅特漢方程,簡稱Hfr方程,它是以三個在分子軌道法發展過程中做出卓著貢獻的人的姓命名的方程。1928年D.R.哈特里提出了一個將 N個電子體系中的每一個電子都看成是在由其餘的 N-1個電子所提供的平均勢場中運動的假設。這樣對於體系中的每一個電子都得到了一個單電子方程(表示這個電子運動狀態的量子力學方程),稱為哈特里方程。使用自洽場疊代方式求解這個方程(見自洽場分子軌道法),就可得到體系的電子結構和性質。
哈特里方程未考慮由於電子自鏇而需要遵守的泡利原理。1930年,B.A.福克和J.C.斯萊特分別提出了考慮泡利原理的自洽場疊代方程,稱為哈特里-福克方程。它將單電子軌函式(即分子軌道)取為自鏇軌函式(即電子的空間函式與自鏇函式的乘積)。泡利原理要求,體系的總電子波函式要滿足反對稱化要求,即對於體系的任何兩個粒子的坐標的交換都使總電子波函式改變正負號,而斯萊特行列式波函式正是滿足反對稱化要求的波函式。
將哈特里-福克方程用於計算多原子分子,會遇到計算上的困難。C.C.J.羅特漢提出將分子軌道向組成分子的原子軌道(簡稱AO)展開,這樣的分子軌道稱為原子軌道的線性組合(簡稱LCAO)。使用LCAO-MO,原來積分微分形式的哈特里-福克方程就變為易於求解的代數方程,稱為哈特里-福克-羅特漢方程,簡稱HFR方程。
RHF 方程 閉殼層體系是指體系中所有的電子均按自鏇相反的方式配對充滿某些殼層(殼層指一個分子能級或能量相同的即簡併的兩個分子能級)。這種體系的特點,是可用單斯萊特行列式表示多電子波函式(分子的狀態),描述這種體系的HFR方程稱為限制性的HFR方程,所謂限制性,是要求每一對自鏇相反的電子具有相同的空間函式。限制性的HFR方程簡稱RHF方程。
UHF 方程 開殼層體系是指體系中有未成對的電子(即有的殼層未充滿)。描述開殼層體系的波函式一般應取斯萊特行列式的線性組合,這樣,計算方案就將很複雜。然而對於開殼層體系的對應極大多重度(所謂多重度,指一個分子因總自鏇角動量的不同而具有幾個能量相重的狀態)的狀態(即自鏇角動量最大的狀態)來說,可以保持波函式的單斯萊特行列式形式(近似方法)。描述這類體系的最常用的方法是假設自鏇向上的電子(α自鏇)和自鏇向下的電子(β自鏇)所處的分子軌道不同,即不限制自鏇相反的同一對電子填入相同的分子軌道。這樣得到的HFR方程稱為非限制性的HFR方程,簡稱UHF方程。
從頭計算法 原則上講,有了HFR方程(不論是RHF方程或是UHF方程),就可以計算任何多原子體系的電子結構和性質。真正嚴格的計算稱之為從頭計算法。RHF方程的極限能量與非相對論薛丁格方程的嚴格解之差稱為相關能。對於某些目的,還需要考慮體系的相關能。UHF方程考慮了相關能的一小部分,更精密的作法則須取多斯萊特行列式的線性組合形式的波函式,由變分法求得這些斯萊特行列式的組合係數。這些由一個斯萊特行列式或數個斯萊特行列式按某種方式組合所描述的分子的電子結構稱為組態,所以這種取多斯萊特行列式波函式的方法稱為組態相互作用法(簡稱CI)。
甚至是對於單行列式的RHF方程和UHF方程的從頭計算法,計算工作量也是驚人的,主要的困難是RHF方程和UHF方程中的電子間排斥積分的計算,這些排斥積分數目多而且計算繁。這樣就有了一些針對簡化排斥積分計算的方案,稱為近似計算方法。近似的RHF方程和UHF方程一般得到的結果較差。取一些經驗參量代替近似 RHF方程和UHF方程中的一些積分,同時忽略某些積分,則能得到令人滿意的結果。這種方法稱為半經驗近似計算方法。
在從頭計算法裡,分子軌道由組成體系的原子的全部原子軌道線性組合而成。對於原子軌道(也稱基組),有不同的選法。斯萊特型軌道適於描寫電子云的分布,但在計算一些積分時包含對無窮級數的積分,十分麻煩,所以在從頭計算法裡,常取高斯型函式做為基函式,取一個高斯型函式或數個高斯型函式的線性組合模擬一個原子軌道。已經有了不少進行多原子體系的從頭計算法的標準的電腦程式,如J.A.波普爾的研究集體推出的電腦程式系列:高斯系列(因其將原子軌道的斯萊特型軌道展開為高斯型軌道,故名)。該系列第一個公開的版本為高斯70(70指1970年),以後差不多每兩年更新一次,現已出到高斯82,功能逐次增多,算法也日趨完善。
贗勢價軌道從頭算法 從直觀的化學觀念出發,可以想見,在原子形成分子時,僅僅原子的價層電子發生了較大的變形,而內層電子分布則改變較小。為了節省計算時間,而又不失去計算精度,從20世紀70年代以來,開始出現只考慮原子的價電子,而把內層電子和原子核看成一個凝固的原子實,用一個模型勢來代替內層電子與價電子的相互作用的從頭計算法,稱為贗勢價軌道從頭算法。不同的方案對於贗勢的取法不盡相同,且大都能得到與全電子從頭算法相近的結果,因而大大節省了計算時間,特別是對於含有重原子的體系,恰好是全電子從頭算難以處理的。贗勢價軌道從頭算法將會在過渡金屬絡合催化的量子化學研究方面發揮重要作用。
組態相互作用法 比從頭算法精確度更高的組態相互作用法有兩個顯著的優點:一是不依賴於試探波函式的形式,就能在原則上提供非相對論薛丁格方程的精確解;二是原則上可用於原子或分子體系的任何穩定態。組態相互作用的概念是相當簡單的,只是將線性變分原理直接用於寫成多行列式線性組合的試探函式,而這些行列式又是單電子軌道的反對稱化乘積,就可以進行CI計算。從原理上講,這種做法對於開殼層幾乎就象對於基態那么容易;對於激發態幾乎就象對於基態那么容易;對於遠離平衡的幾何構型幾乎就象在平衡點附近那么容易。但實際上,除了疊代收斂上的困難外,CI計算還不象從頭計算法那么容易掌握。CI計算需要考慮原子基組、分子軌道和組態函式(簡稱CF,即滿足自鏇匹配,有時還要滿足對稱性匹配的斯萊特行列式或斯萊特行列式的線性組合)的選擇。由於對分子軌道和組態函式CF有不同的選擇,所以有不同的組態相互作用等級。同時最佳化分子軌道和組態函式的組合係數(分子軌道向原子軌道展開,體系總波函式向組態函式展開)的方法稱為多組態自洽場法(簡稱MCSCF法)。組態相互作用法和多組態自洽場法在原子光譜、電子-原子散射和其他原子體系以及范德瓦耳斯力的研究上是非常重要而有用的。
近似計算法 在量子化學半經驗計算方法裡,一般基組都只取價原子軌道,引入一些近似方法,忽略掉全部三中心積分、四中心積分和部分雙中心積分。由於沒有多中心(三中心、四中心)積分的計算困難,所以半經驗近似自洽場方法的原子軌道基組一般都取斯萊特型的原子軌道。目前最常用的近似是零微分重疊(簡稱ZDO)近似,即假定某些原子基之間的重疊為零:
φμ(i)φv(i)=δφv
式中φμ和φv為原子軌道基;δφv為克羅內克符號,當μ等於v時,δφv等於1;μ不等於v時,δφv為零。有不同等級的零微分重疊近似。近似程度最高的是全略微分重疊(簡稱CNDO)近似,是J.A.波普爾等在1965年提出的。在CNDO近似里,取所有不同原子軌道之間的重疊都為零。這樣,雙電子排斥積分為:
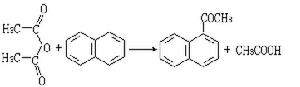
在CNDO法裡,忽略了不同原子軌道上電子的交換相關,因而對兩個具有平行或反平行自鏇的電子間實際存在的不同相互作用未予適當考慮,尤其當兩個電子同屬一個原子時。為了彌補這個缺陷,波普爾等進一步提出了不僅保留單中心庫侖積分,也保留單中心交換積分的方法,稱為間略微分重疊(簡稱INDO)近似法。對於分子的平衡幾何構型,INDO能得到與CNDO相近的結果,而對於分子的波譜(核磁共振和電子自鏇共振譜)的研究,由於考慮了單中心的交換作用,卻能得到CNDO不能得到的結果。
波普爾參量化的CNDO和INDO所得到的能量值都較差。為了使分子的全面性質都能得到好的結果,M.J.S.杜瓦等用一些有代表性的有機分子的實驗生成熱和平衡幾何構型參數做標準,用最小二乘法最佳化出INDO的參量,並用一些函式來代替某些參量,對大部分有機分子,都能同時得到較好的幾何參數和生成熱數值。杜瓦的這種方法稱為改進的INDO法,簡稱MINDO。杜瓦等前後推出三個MINDO版本,分別為MINDO/1、MINDO/2和MINDO/3,其中最成功的並且至今還在較廣泛套用的是MINDO/3。MINDO/3對有些有機分子的生成熱計算甚至能達到化學精度(4~8×103 焦/摩爾)。MINDO/3對一些有機反應的研究也能得到好的結果。
在ZDO近似中,與從頭算最接近的為忽略雙原子微分重疊近似法,簡稱NDDO。它只對屬於不同原子的原子軌道φμ和φv才使用零微分重疊近似,而保留了全部雙中心排斥積分。由於剩下的單中心和雙中心積分的數目還是相當多的,所以計算依然很繁,而得到的結果卻較差,因此很少有人用NDDO進行計算。1977年杜瓦等提出了一個改進的NDDO近似法,稱為MNDO,它採用半經驗模型處理雙中心排斥積分,即把雙原子的電荷分布間的相互作用看成是兩堆電荷分布的多極矩相互作用之和,然後也用實驗數據最佳化參量。這樣,計算時間只比MINDO/3增加百分之二十,而計算結果(與實驗數據相比)卻比MINDO/3好。
在近似計算方法中,還有休克爾分子軌道法和推廣的休克爾分子軌道法。
Xα方法 在量子化學計算方法中,除了MO法和VB法外,還有一種半經驗方法,叫做Xα方法,是斯萊特在1951年首先提出來的。他是將電子交換作用能用一統計平均來近似(用總電子電荷密度乘以某個係數來代替交換能),代入哈特里-福克方程,就得到Xα方程。Xα這個名詞是在推導Xα方程時用的,X指交換能用某種方法近似,同時這個表示式中有一個參數α。
原子和晶體的Xα方程易於求解,由於分子沒有空間周期性,在相當長一段時間內,Xα方程不能用於分子的計算。從1965年以來,發展了多重散射波Xα方法(簡稱SCF-Xα-SW)。用它可求解自洽場方程,首先是用鬆餅罐頭近似,將分子分為三個區:原子內區Ⅰ、原子間區Ⅱ和原子外區Ⅲ。根據Xα方程,分別對三個區域求解,利用邊界條件得到久期方程,從而求得分子軌道和能級。多重散射波Xα方法對原子簇計算結果較好,也比從頭計算法節省計算時間,但計算精度比從頭計算法差。對於三個區域的劃分,需要計算者的經驗和摸索,所以掌握起來比從頭算困難,且套用對象有一定限制(即對於某些分子不大適用)。