定義
在許多生產實際與理論研究中，一個隨機現象常常需要同時用幾個隨機變數去描述，例如，電晶體放大器中某一時刻的噪聲電流就要用隨機振幅和隨機相位兩個隨機變數來表征。又如當一個確定的正弦信號，經過隨機起伏信道傳輸後，到達接收點時其振幅、相位和角頻率已不再是確定的了，而變成隨機參數。這時的信號在某一時刻就要用三個隨機變數來描述。如此可以推廣到”個隨機變數的情況。我們稱n個隨機變數X，X，…，X的總體X=(X，X，…，X)為n維隨機變數(或n元隨機變數)，或稱n維隨機矢量。顯然，一維隨機矢量即為隨機變數。
隨機矢量X的性質不僅由單個隨機變數X，X，…，X的性質所決定，而且還應由這些隨機變數的相互關係所決定。
類似於一維的場合，我們引進如下定義。
稱n元函式：
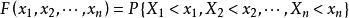聯合分布函式為n維隨機矢量X=((X，X，…，X)的聯合分布函式。它表示事件X<x，X<x。，…，X<x同時出現的機率。
幾何意義
以二維情形為例，以二維情形為例，設（X，Y）是二維隨機變數，x，y是任意實數，二元函式：
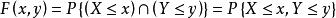聯合分布函式被稱二維隨機變數(X，Y)的分布函式，或稱為X和Y的聯合分布函式。
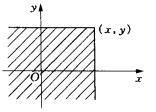
將二維隨機變數（X，Y）看成是平面上隨機點的坐標，分布函式F（x，y）在（x，y）處的函式值就是隨機點（X，Y）落在如圖以（x，y）為頂點而位於該點左下方的無窮矩形區域內的機率。
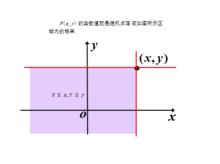聯合分布函式隨機點（X，Y）落在矩形區域
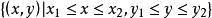聯合分布函式的機率為
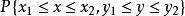聯合分布函式
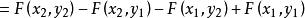聯合分布函式
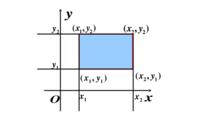聯合分布函式相當於一個大的無窮矩形減去兩個小的無窮矩形，但是多減了一個重合的面積，將它加回來。
基本性質
聯合分布函式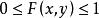
聯合分布函式
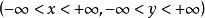聯合分布函式如右圖所示的X和Y的聯合分布函式F(x,y)有如下性質：
(1)，；
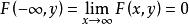聯合分布函式且 ，
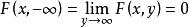聯合分布函式，
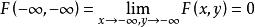聯合分布函式，
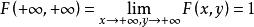聯合分布函式；
(2)F(x，y)關於x(或y)是單調非降的，
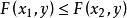聯合分布函式即對固定的y，當x<x時 ，
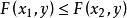聯合分布函式對於固定的x，當y<y ；
(3)F(x，y)關於x(或y)均為右連續的的，即
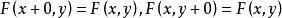聯合分布函式(4)對於任意實數x，x，y，y，(x≤x≤x，y≤y≤y)，下述不等式恆成立
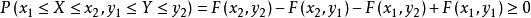聯合分布函式套用舉例
確定係數A、B、C，使二元函式
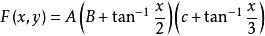聯合分布函式為二維分布函式．
解:由分布函式的性質，有
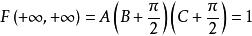聯合分布函式
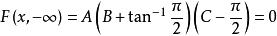聯合分布函式
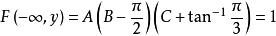聯合分布函式
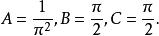聯合分布函式由此可得
