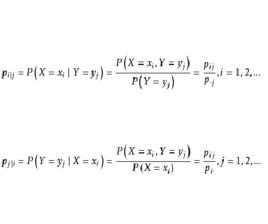定義
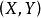條件分布
條件分布
條件分布二維隨機向量 中， 與 的相互關係除了獨立以外，還有相依關係，即隨機變數的取值往往彼此是有影響的，這種關係用條件分布能更好地表達出來。
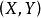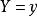條件分布
條件分布對於二維隨機向量 ，所謂隨機變數X的條件分布，就是在 的條件下X的分布函式。比如，記X為人的體重，Y為人的身高，則X與Y一般有相依關係，現在如果限定Y=172(cm)，在這個條件下體重X的分布顯然與X的無條件分布有很大不同。
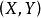條件分布
條件分布
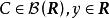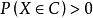條件分布設給定二維隨機向量 ，對任意 ，若 ,則
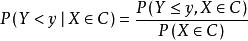條件分布
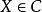條件分布 條件分布是一維分布函式，自然稱它為條件 下， 的條件分布函式。
離散隨機向量的條件分布
條件分布列
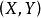條件分布如果二維離散隨機向量 的聯合分布列為
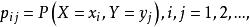條件分布仿照條件機率的定義，我們很容易地給出離散隨機向量的條件分布列。
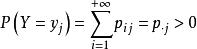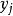條件分布
條件分布定義1 對一切使得 的 ，稱
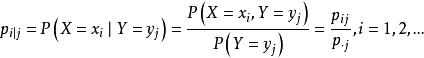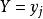條件分布
條件分布為在 給定 條件下X的條件分布列。
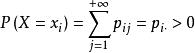條件分布
條件分布同理，對一切使得 的 ，稱
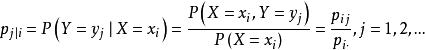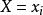條件分布
條件分布為在 給定 條件下Y的條件分布列。
條件分布函式
有了條件分布列，我們就可以定義離散隨機向量的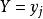條件分布。
條件分布定義2 在給定 條件下X的 條件分布函式為
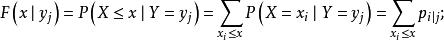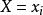條件分布 條件分布在給定 條件下Y的 條件分布函式為
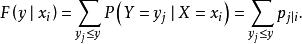條件分布連續隨機向量的條件分布
條件分布函式與條件密度函式
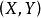條件分布
條件分布
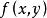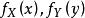條件分布設 為連續型隨機向量，聯合密度函式為 ，邊際分布函式分別為。
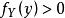條件分布
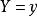條件分布 條件分布定義3 對於一切 的 ，在給定 條件下，X的條件分布函式和條件密度函式分別為
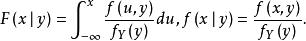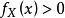條件分布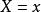
條件分布
條件分布同理對於一切 的x，在給定 條件下，Y的條件分布函式和條件密度函式分別為
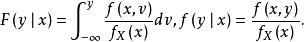條件分布連續場合的全機率公式與貝葉斯公式
有了條件分布密度函式的機率，可以順便給出連續隨機變數場合的全機率公式和貝葉斯公式。
全機率公式
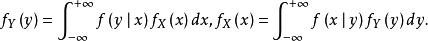條件分布貝葉斯公式
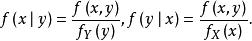條件分布