二維常態分配

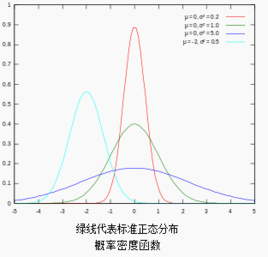
二維常態分配，又名高斯分布（英語：Gaussian distribution，採用德國數學家卡爾·弗里德里希·高斯的名字冠名），是一個在數學、物理及工程等領域都非常重要的機率分布，由於這個分布函式具有很多非常漂亮的性質，使得其在諸多涉及統計科學離散科學等領域的許多方面都有著重大的影響力。比如圖像處理中最常用的濾波器類型為Gaussian濾波器（也就是所謂的常態分配函式）。

基本信息

• 中文名：二維常態分配
• 英文名：two-dimensional normal distribution

• 別稱：高斯分布
• 套用學科：統計學
• 適用領域範圍：數學、物理及工程 、機率論等

定律定義

滿足下述的機率密度分布的隨機變數分布叫做二維常態分配：

其中都是常數，我們稱服從參數為的二維常態分配，常把這個分布記作）。的範圍分別為。這個函式在三維空間中的圖像好像是一個橢圓切面的鐘倒扣在平面上，其中心在（）點。

公式驗證

證明該函式是一個機率密度函式，其應該滿足機率密度函式的基本性質：一是大於零，二是全空間上的積分等於1。第一點顯而易見，下面給出條件二的證明。
做變換
得再做變數代換注意到得

邊緣機率密度

二維常態分配的兩個邊緣分布都是一維常態分配的形式：

，並且都不依賴於參數，即不同的對應不同的二維常態分配，但它們的邊緣分布是一樣的。這一事實表明，單由關於X和關於Y的邊緣分布，不能確定隨機變數X和Y的聯合分布，但加入了結合緊密程度的參數，就可以確定。證明是一維常態分配由於於是令則有同理

獨立性

對於二維正態隨機變數（X，Y），X和Y相互獨立的充要條件是參數ρ=0。必要性：如果ρ=0有充分性：如果X和Y相互獨立，由於都是連續函式，有。特別令。得到為使這一等式成立，從而ρ=0。