邊緣分布
[marginal distribution]
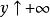邊緣分布函式
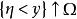邊緣分布函式邊緣分布亦稱邊沿分布或邊際分布。隨機向量中分量各自的機率分布。在（ξ，η）的聯合分布函式定義中，令 ，則事件 。利用機率的下連續性便得ξ 的分布函式
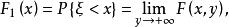邊緣分布函式稱為ξ 的邊緣分布函式（marginal distribution function）。同理η 的邊緣分布函式為
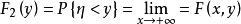邊緣分布函式
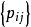邊緣分布函式“邊緣”一詞來源於離散型情形。在二維離散機率分布 的列表表示中，將各行求和寫在表的最右一列，再將各列求和寫在表的最下一行。由於
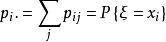邊緣分布函式
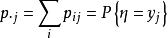邊緣分布函式
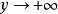邊緣分布函式因此位於表中右邊與下邊的數列分別是ξ 與η 各自的分布。故稱為邊緣分布。對連續型隨機向量（ξ，η），在聯合分布函式定義中 得ξ 的邊緣分布函式
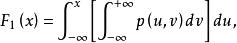邊緣分布函式故分量ξ 仍為連續型。有邊緣密度函式（marginal density function）
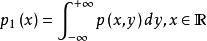邊緣分布函式。
同理，分量η 也是連續型的，其邊緣密度函式為
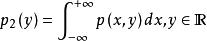邊緣分布函式。
可見，分量的邊緣分布由聯合分布完全確定。但是逆命題不真。
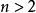邊緣分布函式
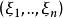邊緣分布函式
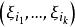邊緣分布函式有例子表明，相同的邊緣分布可構成不同的聯合分布，這反映出兩個分量的結合方式不同，相依程度不同。這種差異在各自的邊緣分布中沒有表現，因而必須考察其聯合分布。對於 的高維情形， 的任何 k 維子向量 的分布稱作 k 維邊緣分布。可用類似二維的方法求出多維情形的邊緣分布。
連續型
如果二維隨機變數X,Y的分布函式F{x,y}為已知，那么
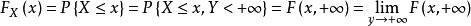邊緣分布函式
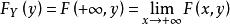邊緣分布函式同理，
因此邊緣分布函式F(x)，F(y)可以由(X,Y)的分布函式所確定。離散型
設離散型隨機變數(X,Y)的分布律p(i=1,2,...；j=1,2,...)則有
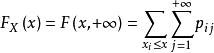邊緣分布函式
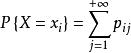邊緣分布函式
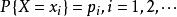邊緣分布函式X的分布律 ，記為
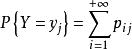邊緣分布函式
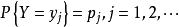邊緣分布函式同理，Y的分布律 ，記為
