一些數據
我們從一個虧格 g的連通緊黎曼曲面開始,在上面取定一點 P。我們想知道極點只在 P的函式。這是向量空間的一個遞增序列:沒有極點的函式(即常值函式),在 P有單極點,在 P點最多有兩個極點,三個極點……這些空間都是有限維的。在 g=0 我們可知維數的序列前幾項為
1, 2, 3, ...:
這可由部分分式理論得出。反之,如果此序列開始為
1, 2, ...
則 g必然是零(所謂黎曼球面)。
由橢圓函式理論知, g=1 時此序列是
1, 1, 2, 3, 4, 5 ...
且這也刻畫了 g=1 情形。當 g> 2 時,序列前端不是固定的;但我們可以確定此序列的後端。我們也可以看到為什麼 g=2 的情形是特殊的,由超橢圓曲線理論,其序列開始幾項為
1, 1, 2, ...
這些結論為何具有這種形式可以追溯到此定理的表述(羅赫的部分):兩個維數之差。當其中一個可以為零,我們得到一個確定的公式,對虧格與度數(即自由度的個數)是線性的。這些例子已經可重構出如下形式
維數 − 修正項 = 度數 −g+ 1。
對 g= 1,修正項當度數為 0 時是 1;其它情形是 0。整個定理說明修正項是函式空間的一個“補空間”的維數。
定理的陳述
用現代記法,虧格為 g的緊黎曼曲面與一個典範除子 K的黎曼–羅赫定理表述為:
l(D) −l(K−D) =deg(D) −g+ 1.
這對所有除子 D均成立。除子是曲面上點的自由阿貝爾群中一個元素。等價地,一個除子是曲面上一些點的整係數線性組合。
我們定義一個亞純函式 f的除子為
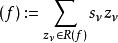 黎曼一羅赫定理
黎曼一羅赫定理這裡 R( f) 是所有零點與極點的集合,而 s定義為
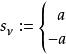 黎曼一羅赫定理 黎曼一羅赫定理 | ,如果 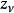 黎曼一羅赫定理 黎曼一羅赫定理 |
,如果 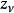 黎曼一羅赫定理 黎曼一羅赫定理 |
我們類似地定義一個亞純1-形式的除子。一個整體亞純函式的除子叫做主除子。相差一個主除子的兩個除子稱為線性等價。一個整體亞純 1-形式的除子叫做典範除子(通常記作 K)。任何兩個亞純 1-形式都是線性等價的,所以典範除子線上性等價的意義下是惟一的。
符號 deg( D) 表示除子 D的度數,即在 D中出現的係數之和。可以證明一個整體亞純函式的除子的度數總是 0,所以除子的度數隻取決於線性等價類。
數 l(D) 是首先感興趣的量:使得 ( h) + D的所有係數都是非負的曲面上亞純函式 h組成的向量空間的維數(在 C上)。直覺上,我們可以將其想像為在每一點處的極點不比 D中對應係數更壞的所有亞純函式;如果在 z處 D的係數是負數,則我們要求 h在 z處至少有那個重數的零點;如果 D的係數是正數, h最多有那個階數的極點。線性等價的除子相應的向量空間通過乘以那個整體亞純函式(這在差一個常數下是良定義的)是自然同構的。
即便我們對 K一無所知,我們知道 特殊性指標( index of speciality)(上文所說的修正項)
l(K−D) ≥ 0,
所以
l(D) ≥deg(D) −g+ 1
這就是早先提到的 黎曼不等式。
上面定理對所有緊連通黎曼曲面都成立。這個公式對一個代數閉域 k上所有非奇異射影代數曲線也成立。這裡 l( D) 表示在每一點的極點不坏於 D中對應係數的曲線上有理函式空間的維數(在 k上)。
為了將其與我們上面的例子聯繫起來,我們需要 K的一些信息:對 g=1 我們可取 K=0,而對 g=0 可取 K= −2 P(任何 P)。一般地 K的度數是 2 g− 2。只要 D的度數至少是 2 g− 1 我們可確保修正項是 0。
回到 g= 2 的情形我們可知上面提到的序列是
1, 1,?, 2, 3, ... .
由此知度數為 2 的不確定項是 1 或 2,當然與點的選擇有關。可以證明任何虧格為 2 的曲線恰有六個點的序列是 1, 1, 2, 2, ... 而其它一般點的序列是 1, 1, 1, 2, ...。特別地,一個虧格 2 曲線是超橢圓曲線。對 g>2 幾乎所有點的序列以 g+1個 1 開始,只有有限個點為其它序列(參見魏爾斯特拉斯點)。
推廣
曲線的黎曼–羅赫定理對黎曼曲面由黎曼與羅赫於1850年代證明,對代數曲線由施密特於1929年證明。它是基本的,曲線後續理論試圖加細它的結論(比如布里爾–諾特理論)。
在更高維(適當的定義除子或線叢)此定理有多個版本。它們的一般表述取決於將定理分成兩部分。其一,現在稱為塞爾對偶性,將 l( K− D) 項解釋為第一層同調群的維數, l( D) 為零次上同調群(或截面的空間)的維數,定理左邊成為一個歐拉示性數,而右邊給出它的計算,正好只與黎曼曲面的拓撲有關的一個度數。
在二維代數幾何中這樣一個公式由義大利幾何學派找到;代數曲面的黎曼-羅赫定理證明了(有各種版本,最早可能屬於馬克斯·諾特。這樣的問題大約在1950年前解決了。
n-維推廣,希策布魯赫–黎曼–羅赫定理,由弗里德里希·希策布魯赫找到並證明,利用了代數拓撲學中的示性類;他深受小平邦彥的工作影響。大約在同一時間讓-皮埃爾·塞爾給出了塞爾對偶性的一般形式,故我們冠以他的姓氏。
亞歷山大·格羅滕迪克於1957年證明了一個深遠的推廣,現在叫做格羅滕迪克–黎曼–羅赫定理。他的工作將黎曼–羅赫重新解釋為不僅是關於一個簇的定理,而是關於兩個簇之間的一個態射的。證明的細節由博雷爾–塞爾於1958年發表。
最後在代數拓撲中也找到了一個一般版本。這些發展本質上在1950年至1960年完成。阿蒂亞–辛格指標定理開啟了這一條推廣的道路。
它導致的結論是一個凝聚層相當好計算。如果只對交錯和中一項感興趣,這是通常的情形,必需更進一步的討論比如消滅定理。

