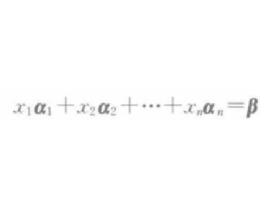定義
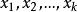 線性組合
線性組合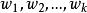 線性組合
線性組合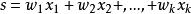 線性組合
線性組合定義一個包含k個實數變數的集合 ,且假設已知一個k個實數權重集合 。我們定義 。s變數是對變數x的加權線性”混合”。因此,將s定義為變數的線性組合。
 線性組合
線性組合可以將線性組合的概念推廣到矢量中。定義每個 是一個矢量,因此,它們的線性組合 s也是一個矢量。當然.每個矢量必須有相同數量的元素。請注意, s的每個分量都是一個由被組合矢量的相對應元素構成的線性組合。
標量的線性組合
定義標量為2,4,1,5,權重為0.1,0.4,0.25,0.25。求其線性組合s。
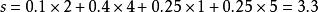 線性組合
線性組合解:線性組合
矢量的線性組合
向量的線性組合屬於矢量的線性組合,下面會詳細介紹。
定義矢量為[2 4 1 5],[3 5 1 2],[5 6 2 1],[9 0 1 3]·權重為0.1,0.4,0.25,0.25。求其線性組合s。
解:線性組合
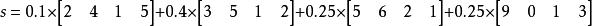 線性組合
線性組合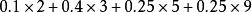 線性組合
線性組合s的第一個元素是。
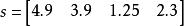 線性組合
線性組合相應地,其他元素分別是3.9,1.25和2.3。因此。
向量組的線性組合
 線性組合
線性組合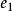 線性組合
線性組合 線性組合
線性組合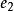 線性組合
線性組合 線性組合
線性組合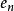 線性組合
線性組合 線性組合
線性組合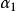 線性組合
線性組合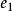 線性組合
線性組合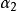 線性組合
線性組合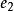 線性組合
線性組合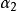 線性組合
線性組合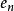 線性組合
線性組合1.任一n維向量 α= ,可由n維單位向量組 = , = ,......, = 線性表示,表達式為 α= + +......+ .
 線性組合
線性組合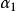 線性組合
線性組合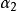 線性組合
線性組合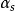 線性組合
線性組合 線性組合
線性組合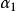 線性組合
線性組合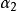 線性組合
線性組合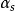 線性組合
線性組合 線性組合
線性組合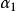 線性組合
線性組合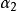 線性組合
線性組合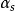 線性組合
線性組合 線性組合
線性組合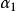 線性組合
線性組合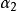 線性組合
線性組合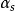 線性組合
線性組合2.設 , , ,…, 為一組n維向量.若存在一組數k₁,k₂,k₃,...,ks使得 =k₁ +k₂ +,…,+ks 為成立,則稱向量 是向量組 , ,…, 的線性組合,或稱向量 可由向量組 , ,…, 線性表示.