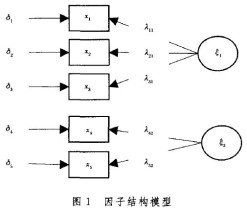
基本介紹
1.主成分分析
主成分分析主要是一種探索性的技術,在分析者進行多元數據分析之前,用他來分析數據,讓自己對數據有一個大致的了解,這是非常有必要的。主成分分析一般很少單獨使用:a、了解數據。(screening the data),b、和cluster analysis(聚類分析)一起使用,c、和判別分析一起使用,比如當變數很多,個案數不多,直接使用判別分析可能無解,這時候可以使用主成分對變數簡化(reduce dimensionality),d、在多元回歸中,主成分分析可以幫助判斷是否存在共線性(條件指數),還可以用來處理共線性。
1、因子分析中是把變數表示成各因子的線性組合,而主成分分析中則是把主成分表示成各變數的線性組合。
2、主成分分析的重點在於解釋各變數的總方差,而因子分析則把重點放在解釋各變數之間的協方差。
3、主成分分析中不需要有假設(assumptions),因子分析則需要一些假設。因子分析的假設包括:各個共同因子之間不相關,特殊因子(specific factor)之間也不相關,共同因子和特殊因子之間也不相關。
4、主成分分析中,當給定的協方差矩陣或者相關矩陣的特徵值是唯一的時候,主成分一般是獨特的;而因子分析中因子不是獨特的,可以鏇轉得到不同的因子。
5、在因子分析中,因子個數需要分析者指定(spss根據一定的條件自動設定,只要是特徵值大於1的因子進入分析),而指定的因子數量不同而結果不同。在主成分分析中,成分的數量是一定的,一般有幾個變數就有幾個主成分。和主成分分析相比,由於因子分析可以使用鏇轉技術幫助解釋因子,在解釋方面更加有優勢。大致說來,當需要尋找潛在的因子,並對這些因子進行解釋的時候,更加傾向於使用因子分析,並且藉助鏇轉技術幫助更好解釋。而如果想把現有的變數變成少數幾個新的變數(新的變數幾乎帶有原來所有變數的信息)來進入後續的分析,則可以使用主成分分析。當然,這種情況也可以使用因子得分做到。所以這種區分不是絕對的。
在算法上,主成分分析和因子分析很類似,不過在因子分析中所採用的協方差矩陣的對角元素不再是變數的方差,而是和變數對應的共同度(變數方差中被各因子所解釋的部分)。
2.聚類分析(Cluster Analysis)
聚類分析是直接比較各事物之間的性質,將性質相近的歸為一類,將性質差別較大的歸入不同的類的分析技術。
在市場研究領域,聚類分析主要套用方面是幫助我們尋找目標消費群體,運用這項研究技術,我們可以劃分出產品的細分市場,並且可以描述出各細分市場的人群特徵,以便於客戶可以有針對性的對目標消費群體施加影響,合理地開展工作。
3.判別分析(Discriminatory Analysis)
判別分析(Discriminatory Analysis)的任務是根據已掌握的1批分類明確的樣品,建立較好的判別函式,使產生錯判的事例最少,進而對給定的1個新樣品,判斷它來自哪個總體。根據資料的性質,分為定性資料的判別分析和定量資料的判別分析;採用不同的判別準則,又有費歇、貝葉斯、距離等判別方法。
費歇(FISHER)判別思想是投影,使多維問題簡化為一維問題來處理。選擇一個適當的投影軸,使所有的樣品點都投影到這個軸上得到一個投影值。對這個投影軸的方向的要求是:使每一類內的投影值所形成的類內離差儘可能小,而不同類間的投影值所形成的類間離差儘可能大。貝葉斯(BAYES)判別思想是根據先驗機率求出後驗機率,並依據後驗機率分布作出統計推斷。所謂先驗機率,就是用機率來描述人們事先對所研究的對象的認識的程度;所謂後驗機率,就是根據具體資料、先驗機率、特定的判別規則所計算出來的機率。它是對先驗機率修正後的結果。
距離判別思想是根據各樣品與各母體之間的距離遠近作出判別。即根據資料建立關於各母體的距離判別函式式,將各樣品數據逐一代入計算,得出各樣品與各母體之間的距離值,判樣品屬於距離值最小的那個母體。
4.對應分析(Correspondence Analysis)
對應分析是一種用來研究變數與變數之間聯繫緊密程度的研究技術。
運用這種研究技術,我們可以獲取有關消費者對產品品牌定位方面的圖形,從而幫助您及時調整行銷策略,以便使產品品牌在消費者中能樹立起正確的形象。
這種研究技術還可以用於檢驗廣告或市場推廣活動的效果,我們可以通過對比廣告播出前或市場推廣活動前與廣告播出後或市場推廣活動後消費者對產品的不同認知圖來看出廣告或市場推廣活動是否成功的向消費者傳達了需要傳達的信息。
5.典型相關分析
典型相關分析是分析兩組隨機變數間線性密切程度的統計方法,是兩變數間線性相關分析的拓廣。各組隨機變數中既可有定量隨機變數,也可有定性隨機變數(分析時須F6說明為定性變數)。本法還可以用於分析高維列聯表各邊際變數的線性關係。
注意
1.嚴格地說,一個典型相關係數描述的只是一對典型變數之間的相關,而不是兩個變數組之間的相關。而各對典型變數之間構成的多維典型相關才共同揭示了兩個觀測變數組之間的相關形式。
2.典型相關模型的基本假設和數據要求
要求兩組變數之間為線性關係,即每對典型變數之間為線性關係;
每個典型變數與本組所有觀測變數的關係也是線性關係。如果不是線性關係,可先線性化:如經濟水平和收入水平與其他一些社會發展水之間並不是線性關係,可先取對數。即log經濟水平,log收入水平。
3.典型相關模型的基本假設和數據要求
所有觀測變數為定量數據。同時也可將定性數據按照一定形式設為虛擬變數後,再放入典型相關模型中進行分析。
6.多維尺度分析(Multi-dimension Analysis)
多維尺度分析(Multi-dimension Analysis) 是市場研究的一種有力手段,它可以通過低維空間(通常是二維空間)展示多個研究對象(比如品牌)之間的聯繫,利用平面距離來反映研究對象之間的相似程度。由於多維尺度分析法通常是基於研究對象之間的相似性(距離)的,只要獲得了兩個研究對象之間的距離矩陣,我們就可以通過相應統計軟體做出他們的相似性知覺圖。
在實際套用中,距離矩陣的獲得主要有兩種方法:一種是採用直接的相似性評價,先將所有評價對象進行兩兩組合,然後要求被訪者所有的這些組合間進行直接相似性評價,這種方法我們稱之為直接評價法;另一種為間接評價法,由研究人員根據事先經驗,找出影響人們評價研究對象相似性的主要屬性,然後對每個研究對象,讓被訪者對這些屬性進行逐一評價,最後將所有屬性作為多維空間的坐標,通過距離變換計算對象之間的距離。
多維尺度分析的主要思路是利用對被訪者對研究對象的分組,來反映被訪者對研究對象相似性的感知,這種方法具有一定直觀合理性。同時該方法實施方便,調查中被訪者負擔較小,很容易得到理解接受。當然,該方法的不足之處是犧牲了個體距離矩陣,由於每個被訪者個體的距離矩陣只包含1與0兩種取值,相對較為粗糙,個體距離矩陣的分析顯得比較勉強。但這一點是完全可以接受的,因為對大多數研究而言,我們並不需要知道每一個體的空間知覺圖。
多元統計分析是統計學中內容十分豐富、套用範圍極為廣泛的一個分支。在自然科學和社會科學的許多學科中,研究者都有可能需要分析處理有多個變數的數據的問題。能否從表面上看起來雜亂無章的數據中發現和提煉出規律性的結論,不僅對所研究的專業領域要有很好的訓練,而且要掌握必要的統計分析工具。對實際領域中的研究者和高等院校的研究生來說,要學習掌握多元統計分析的各種模型和方法,手頭有一本好的、有長久價值的參考書是非常必要的。這樣一本書應該滿足以下條件:首先,它應該是“淺入深出”的,也就是說,既可供初學者入門,又能使有較深基礎的人受益。其次,它應該是既側重於套用,又兼顧必要的推理論證,使學習者既能學到“如何”做,而且在一定程度上了解“為什麼”這樣做。最後,它應該是內涵豐富、全面的,不僅要基本包括各種在實際中常用的多元統計分析方法,而且還要對現代統計學的最新思想和進展有所介紹、交代。
主成分分析通過線性組合將原變數綜合成幾個主成分,用較少的綜合指標來代替原來較多的指標(變數)。在多變數分析中,某些變數間往往存在相關性。是什麼原因使變數間有關聯呢?是否存在不能直接觀測到的、但影響可觀測變數變化的公共因子?因子分析法(Factor Analysis)就是尋找這些公共因子的模型分析方法,它是在主成分的基礎上構築若干意義較為明確的公因子,以它們為框架分解原變數,以此考察原變數間的聯繫與區別。
例如,隨著年齡的增長,兒童的身高、體重會隨著變化,具有一定的相關性,身高和體重之間為何會有相關性呢?因為存在著一個同時支配或影響著身高與體重的生長因子。那么,我們能否通過對多個變數的相關係數矩陣的研究,找出同時影響或支配所有變數的共性因子呢?因子分析就是從大量的數據中“由表及里”、“去粗取精”,尋找影響或支配變數的多變數統計方法。
可以說,因子分析是主成分分析的推廣,也是一種把多個變數化為少數幾個綜合變數的多變數分析方法,其目的是用有限個不可觀測的隱變數來解釋原始變數之間的相關關係。
因子分析主要用於:1、減少分析變數個數;2、通過對變數間相關關係探測,將原始變數進行分類。即將相關性高的變數分為一組,用共性因子代替該組變數。
統計意義
模型中F1,F2,…,Fm叫做主因子或公共因子,它們是在各個原觀測變數的表達式中都共同出現的因子,是相互獨立的不可觀測的理論變數。公共因子的含義,必須結合具體問題的實際意義而定。e1,e2,…,ep叫做特殊因子,是向量x的分量xi(i=1,2,…,p)所特有的因子,各特殊因子之間以及特殊因子與所有公共因子之間都是相互獨立的。模型中載荷矩陣A中的元素(aij)是為因子載荷。因子載荷aij是xi與Fj的協方差,也是xi與Fj的相關係數,它表示xi依賴Fj的程度。可將aij看作第i個變數在第j公共因子上的權,aij的絕對值越大(|aij|£1),表明xi與Fj的相依程度越大,或稱公共因子Fj對於xi的載荷量越大。為了得到因子分析結果的經濟解釋,因子載荷矩陣A中有兩個統計量十分重要,即變數共同度和公共因子的方差貢獻。
因子載荷矩陣A中第i行元素之平方和記為hi2,稱為變數xi的共同度。它是全部公共因子對xi的方差所做出的貢獻,反映了全部公共因子對變數xi的影響。hi2大表明x的第i個分量xi對於F的每一分量F1,F2,…,Fm的共同依賴程度大。
將因子載荷矩陣A的第j列( j =1,2,…,m)的各元素的平方和記為gj2,稱為公共因子Fj對x的方差貢獻。gj2就表示第j個公共因子Fj對於x的每一分量xi(i= 1,2,…,p)所提供方差的總和,它是衡量公共因子相對重要性的指標。gj2越大,表明公共因子Fj對x的貢獻越大,或者說對x的影響和作用就越大。如果將因子載荷矩陣A的所有gj2 ( j =1,2,…,m)都計算出來,使其按照大小排序,就可以依此提煉出最有影響力的公共因子。
3. 因子鏇轉
建立因子分析模型的目的不僅是找出主因子,更重要的是知道每個主因子的意義,以便對實際問題進行分析。如果求出主因子解後,各個主因子的典型代表變數不很突出,還需要進行因子鏇轉,通過適當的鏇轉得到比較滿意的主因子。
鏇轉的方法有很多,正交鏇轉(orthogonal rotation)和斜交鏇轉(oblique rotation)是因子鏇轉的兩類方法。最常用的方法是最大方差正交鏇轉法(Varimax)。進行因子鏇轉,就是要使因子載荷矩陣中因子載荷的平方值向0和1兩個方向分化,使大的載荷更大,小的載荷更小。因子鏇轉過程中,如果因子對應軸相互正交,則稱為正交鏇轉;如果因子對應軸相互間不是正交的,則稱為斜交鏇轉。常用的斜交鏇轉方法有Promax法等。
4.因子得分
因子分析模型建立後,還有一個重要的作用是套用因子分析模型去評價每個樣品在整個模型中的地位,即進行綜合評價。例如地區經濟發展的因子分析模型建立後,我們希望知道每個地區經濟發展的情況,把區域經濟劃分歸類,哪些地區發展較快,哪些中等發達,哪些較慢等。這時需要將公共因子用變數的線性組合來表示,也即由地區經濟的各項指標值來估計它的因子得分。
設公共因子F由變數x表示的線性組合為:
Fj = uj1 xj1+ uj2 xj2+…+ujpxjp j=1,2,…,m
該式稱為因子得分函式,由它來計算每個樣品的公共因子得分。若取m=2,則將每個樣品的p個變數代入上式即可算出每個樣品的因子得分F1和F2,並將其在平面上做因子得分散點圖,進而對樣品進行分類或對原始數據進行更深入的研究。
但因子得分函式中方程的個數m小於變數的個數p,所以並不能精確計算出因子得分,只能對因子得分進行估計。估計因子得分的方法較多,常用的有回歸估計法,Bartlett估計法,Thomson估計法。
⑴回歸估計法
F = X b = X (X ¢X)-1A¢ = XR-1A¢ (這裡R為相關陣,且R = X ¢X )。
⑵Bartlett估計法
Bartlett估計因子得分可由最小二乘法或極大似然法導出。
F = [(W-1/2A)¢ W-1/2A]-1(W-1/2A)¢ W-1/2X = (A¢W-1A)-1A¢W-1X
⑶Thomson估計法
在回歸估計法中,實際上是忽略特殊因子的作用,取R = X ¢X,若考慮特殊因子的作用,此時R = X ¢X+W,於是有:
F = XR-1A¢ = X (X ¢X+W)-1A¢
這就是Thomson估計的因子得分,使用矩陣求逆算法(參考線性代數文獻)可以將其轉換為:
F = XR-1A¢ = X (I+A¢W-1A)-1W-1A¢