線上性代數中,向量是有活力的計算單元。向量能組成向量組,構成矩陣,建立向量子空間,並實現各類向量計算。多個向量集成的向量組可構造矩陣,方陣的行列式是求矩陣的數量。三個數據元的表示方法是多樣的。
def1.1 n維向量
設a1,a2,…, an是n個數,由這幾個數組成的有序數組(a1,a2,…, an)稱為一個n維向量。數a1,a2,…, an稱為向量分量。
[說明]:①常用
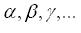 向量表示(變數)
向量表示(變數)向量表示
表示向量。
②不說明向量都是n維。
③.向量分量的關係沒有固定規則。然而向量的來源很多:性質相同的一組數;同一事物的不同屬性。例如:一個月內的溫度數據,可構成一個向量。例如:方程組中任一未知量係數構成一個向量,即向量可套用於方程組求解。一個形式完備的非齊次線性方程組(計算式)可用增廣矩陣
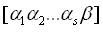 向量組構造的增廣矩陣
向量組構造的增廣矩陣向量組構造的增廣矩陣
表示 ,稱為計算式的集合簡化形式。構成係數列向量的分量因為公共解集之間。
構造向量後可實現向量計算(向量加法與數乘),例如向量組的線性組合(複合計算):
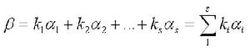 向量的線性組合計算
向量的線性組合計算向量的線性組合計算
&向量的表示方法.
1符號表示方法
①常量α,變數x .
2單向量具體表示方法
②轉置表示
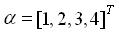 列向量轉置表示
列向量轉置表示列向量轉置表示
; α= (1,2,3,4)行向量;
列向量表示:
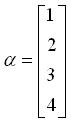 列向量
列向量列向量
.
3單向量的計算式表示方法
③線性組合:
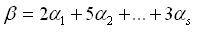 向量的線性組合表達式
向量的線性組合表達式向量的線性組合表達式
④向量的矩陣乘:
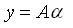 向量的矩陣乘法表示
向量的矩陣乘法表示向量的矩陣乘法表示
4向量集合表示方法
⑤變數x屬於某一個向量集合,只用一個變數x代表一個集合。
⑥向量組枚舉表示:
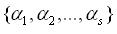 枚舉集合表示
枚舉集合表示枚舉集合表示
,
可簡記為
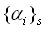 簡化表示
簡化表示簡化表示
⑦變係數線性組合
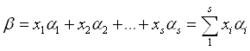 變係數
變係數變係數
,其中數
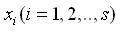 簡化表示
簡化表示簡化表示
屬於某一個實數域是變數數,當組合係數變數取不同值時可表示不同的向量,因此能夠表示一個向量集合.
⑧矩陣:
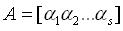 矩陣的向量表示
矩陣的向量表示矩陣的向量表示
⑨向量空間
⑩生成(子)空間
[說明]:
1.從該集合中給x賦不同值,則用一個變數代替了這個集合的所有向量,因此是集合表示方法。有些變數只有一個值,所以不是集合表示,與用法⑤不同。
2.矩陣可由一個向量組構造,但並不是一個向量組.
3.在公式表示法中,可以先給向量賦值再計算,也可以先化簡再帶入具體值.所以計算式表示法,向量可是抽象形式也可是具體值形式.
4⑥⑦都是集合的表示方法,⑥是枚舉表示方法,一般用在有限離散元素集合。⑦是謂詞表示方法,用元素變數的計算式關係(方程,不等式)表示。枚舉方法簡單直觀,但是有時並不能說明元素構成集合的成因,用謂詞法表示元素功能,完整描述了集合的功能信息。
def1.1.1向量組
s個向量構成的集合,稱為(一個)向量組。
[說明]不同向量組的功能不同。一個向量組可以構成一個向量空間。將向量組的元素排列成一個矩形,稱為矩陣。
def1.2 矩陣
由s*n個數排成s行n列的一個數表,稱為矩陣,常
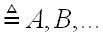 符號表示
符號表示符號表示
,即
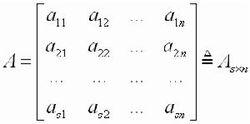 數值表示
數值表示數值表示
。若s=n,則稱為方陣。
[說明]①.矩陣可用簡化形式
簡化表示
,i表示行標(分量序數),j表示列標(向量序數)。AII稱為對角線元素。{aij(j=1,…n)}稱為矩陣的第i行元素,可視為行向量,{aij(i=1,…n)}稱為矩陣的第j列元素, 可視為列向量.
②矩陣是具有隱形式計算的數據元。
a.與階梯形對應的初等變換,可相似或契約對角化。
b.數量。行列式,特徵值(特徵多項式)
c.伴隨矩陣集合={轉置矩陣,逆矩陣,伴隨矩陣;簡化階梯形,相似對角陣或
者契約對角陣}
③常量矩陣
a.0矩陣(加法0元):元素全是零的矩陣稱為零距陣.可記作
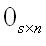 0
0.
b.單位矩陣(乘法不變元):
 單位矩陣
單位矩陣單位矩陣
c.常量矩陣
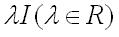 常數矩陣
常數矩陣常數矩陣
d.對角矩陣形如
 對角矩陣(並不是上三角,下三角矩陣)
對角矩陣(並不是上三角,下三角矩陣)對角矩陣(並不是上三角,下三角矩陣)
的方陣稱為對角陣.
④矩陣的結構.
a.可將向量組排列成矩陣,矩陣中可由行向量組或列向量組構成。然而矩陣仍然可以視為由s*n個元素構成的平面數表.
b.行向量組或列向量組構成的二級結構
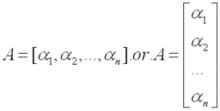 矩陣的向量組結構
矩陣的向量組結構矩陣的向量組結構
.
c.分塊矩陣(子矩陣)構成,可稱為廣義矩陣。
矩陣的結構(劃分partition)是某一類可重構計算的理論基礎,這一類可重構計算的基本單元是相同的,而且也是計算單元粒度劃分的基礎。
⑤矩陣不僅僅是數的集合,而且有位置的排列,稱為結構。因此對類似八皇后的問題可構造相關的矩陣邏輯計算處理。
def1.3 行列式
由n的平方個數排成一個正方形數表,加記號| |.它的值是所有取自不同行不同列的n個元素
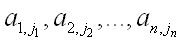 矩陣的型
矩陣的型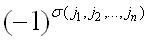 1
1行序列
序列符號的乘積的代數和.代數和的正負號由
.
決定,即可寫成
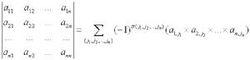 1
1序列展開式
。這裡
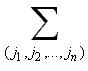 1
1序列的變數表示代數和
表示對列標形成的n階排列
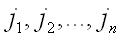 1
1序列變數表示
要遍取所有n階排列時求和,顯然應有項,稱上式為n階行列式的表達式(或稱完全展開式).
.1 n=1,
.2高階行列式
n>3的行列式
[說明] ① 個數排成的一個正方形數表,加記號||,這個數表可視為多維的數量分布,如同密度的不均勻分布。行列式可直接來自矩陣,因此可視為矩陣的數量分布,是矩陣整體數量特徵的提取。
②行列式是有算符的數據結構,運算符||也具有集合符號的功能。

