主成分分析

主成分分析（Principal Component Analysis，PCA）， 將多個變數通過線性變換以選出較少個數重要變數的一種多元統計分析方法。又稱主分量分析。在實際課題中，為了全面分析問題，往往提出很多與此有關的變數（或因素），因為每個變數都在不同程度上反映這個課題的某些信息。主成分分析首先是由K.皮爾森對非隨機變數引入的，爾後H.霍特林將此方法推廣到隨機向量的情形。信息的大小通常用離差平方和或方差來衡量。

基本信息

• 中文名：主成分分析
• 英文名：Principal Component Analysis

• 簡稱：PCA
• 又名：主分量分析

原理

主成分分析

在用統計分析方法研究多變數的課題時，變數個數太多就會增加課題的複雜性。人們自然希望變數個數較少而得到的信息較多。在很多情形，變數之間是有一定的相關關係的，當兩個變數之間有一定相關關係時，可以解釋為這兩個變數反映此課題的信息有一定的重疊。主成分分析是對於原先提出的所有變數，將重複的變數（關係緊密的變數）刪去多餘，建立儘可能少的新變數，使得這些新變數是兩兩不相關的，而且這些新變數在反映課題的信息方面儘可能保持原有的信息。
設法將原來變數重新組合成一組新的互相無關的幾個綜合變數，同時根據實際需要從中可以取出幾個較少的綜合變數儘可能多地反映原來變數的信息的統計方法叫做主成分分析或稱主分量分析，也是數學上用來降維的一種方法。

套用學科

主成分分析作為基礎的數學分析方法，其實際套用十分廣泛，比如人口統計學、數量地理學、分子動力學模擬、數學建模、數理分析等學科中均有套用，是一種常用的多變數分析方法。

成分分析

成分分析（包含成分檢測、成分測試項目）是通過微觀譜圖對未知成分進行分析的技術方法，因該技術普遍採用光譜，色譜，能譜，熱譜，質譜等微觀譜圖。

內容

基本思想

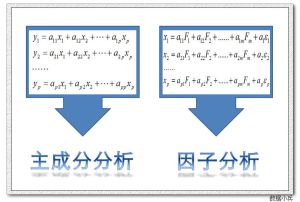主成分分析與因子分析

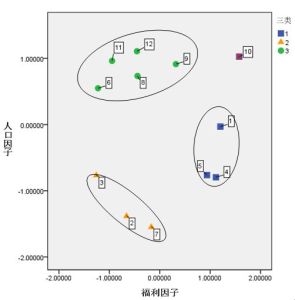
主成分分析是設法將原來眾多具有一定相關性（比如P個指標），重新組合成一組新的互相無關的綜合指標來代替原來的指標。
主成分分析，是考察多個變數間相關性一種多元統計方法，研究如何通過少數幾個主成分來揭示多個變數間的內部結構，即從原始變數中導出少數幾個主成分，使它們儘可能多地保留原始變數的信息，且彼此間互不相關.通常數學上的處理就是將原來P個指標作線性組合，作為新的綜合指標。
最經典的做法就是用F1（選取的第一個線性組合，即第一個綜合指標）的方差來表達，即Var(F1)越大，表示F1包含的信息越多。因此在所有的線性組合中選取的F1應該是方差最大的，故稱F1為第一主成分。如果第一主成分不足以代表原來P個指標的信息，再考慮選取F2即選第二個線性組合，為了有效地反映原來信息，F1已有的信息就不需要再出現在F2中，用數學語言表達就是要求Cov(F1,F2)=0，則稱F2為第二主成分，依此類推可以構造出第三、第四，……，第P個主成分。

步驟

Fp=a1i*ZX1+a2i*ZX2+……+api*ZXp
其中a1i,a2i,……,api(i=1,……,m)為X的協方差陣Σ的特徵值所對應的特徵向量，ZX1,ZX2,……,ZXp是原始變數經過標準化處理的值，因為在實際套用中，往往存在指標的量綱不同，所以在計算之前須先消除量綱的影響，而將原始數據標準化，本文所採用的數據就存在量綱影響[註：本文指的數據標準化是指Z標準化。
主成分分析法的計算步驟
主成分分析法的計算步驟
A=(aij)p×m=(a1,a2,…am,)，
Rai=λiai，
R為相關係數矩陣，λi、ai是相應的特徵值和單位特徵向量,λ1≥λ2≥…≥λp≥0。
進行主成分分析主要步驟如下：
1.指標數據標準化（SPSS軟體自動執行）；
2.指標之間的相關性判定；
3.確定主成分個數m；
4.主成分Fi表達式；
5.主成分Fi命名；