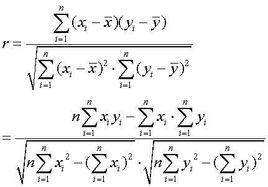定義
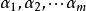線性相關在向量空間V的一組向量 A : ，如果存在 不全為零的數 k, k, ···,k , 使
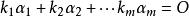線性相關則稱向量組 A是線性相關的 ，否則數 k, k, ···,km全為0時稱它是線性無關。
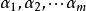線性相關由此定義看出 是否線性相關，就看是否存在一組 不全為零的數 k, k, ···,k使得上式成立。
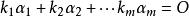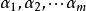線性相關 線性相關即是看這個齊次線性方程組是否存在非零解，將其係數矩陣化為最簡形矩陣，即可求解。此外，當這個齊次線性方程組的係數矩陣是一個方陣時，這個係數矩陣存在行列式為0，即有非零解，從而 線性相關。
注意
對於任一向量組而言,，不是線性無關的就是線性相關的。
向量組只包含一個向量a時，a為0向量，則說A線性相關; 若a≠0, 則說A線性無關。
包含零向量的任何向量組是線性相關的。
含有相同向量的向量組必線性相關。
增加向量的個數，不改變向量的相關性。(注意，原本的向量組是線性相關的)
【局部相關，整體相關】
減少向量的個數，不改變向量的無關性。(注意，原本的向量組是線性無關的）
【整體無關，局部無關】
一個向量組線性無關，則在相同位置處都增加一個分量後得到的新向量組仍線性無關。
【無關組的加長組仍無關】
一個向量組線性相關，則在相同位置處都去掉一個分量後得到的新向量組仍線性相關。
【相關組的縮短組仍相關】
若向量組所包含向量個數等於分量個數時，判定向量組是否線性相關即是判定這些向量為列組成的行列式是否為零。若行列式為零，則向量組線性相關；否則是線性無關的。
1.對於任一向量組而言,，不是線性無關的就是線性相關的。
2.一個
3.包含零向量的任何向量組是線性相關的。
4.含有相同向量的向量組必線性相關。
5.增加向量的個數，不改變向量的相關性。(注意，原本的向量組是線性相關的)
【局部相關，整體相關】
6.減少向量的個數，不改變向量的無關性。(注意，原本的向量組是線性無關的）
【整體無關，局部無關】
7.一個向量組線性無關，則在相同位置處都增加一個分量後得到的新向量組仍線性無關。
【無關組的加長組仍無關】
8.一個向量組線性相關，則在相同位置處都去掉一個分量後得到的新向量組仍線性相關。
【相關組的縮短組仍相關】
9.若向量組所包含向量個數等於分量個數時，判定向量組是否線性相關即是判定這些向量為列組成的行列式是否為零。若行列式為零，則向量組線性相關；否則是線性無關的。
定理
1、向量 a, a, ···, an(n≧2)線性相關的充要條件是這n個向量中的一個為其餘(n-1)個向量的線性組合。
2、一個向量線性相關的充分條件是它是一個零向量。
3、兩個向量 a、 b共線的充要條件是 a、 b線性相關 。
4、三個向量 a、 b、 c共面的充要條件是 a、 b、 c線性相關。
5、n+1個n維向量總是線性相關。【個數大於維數必相關】
