定義1
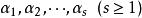 最大線性無關組
最大線性無關組 最大線性無關組
最大線性無關組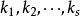 最大線性無關組
最大線性無關組向量組 稱為線性相關,如果有數域 中不全為零的數 ,使得
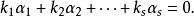 最大線性無關組
最大線性無關組定義2
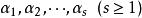 最大線性無關組
最大線性無關組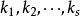 最大線性無關組
最大線性無關組一向量組 不線性相關,即沒有不全為零的數 ,使得
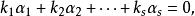 最大線性無關組
最大線性無關組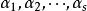 最大線性無關組
最大線性無關組就稱為線性無關;或者說,一向量組稱為線性無關,如果由
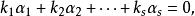 最大線性無關組
最大線性無關組就可以推出
 最大線性無關組
最大線性無關組換個說法,如果一向量組線性無關,那么它的任何一個非空的部分組也線性無關。特別地,由於兩個成比例的向量是線性相關的,所以,線性無關的向量組中一定不能包含兩個成比例的向量。
定義3
一個向量組的一部分組稱為一個 極大線性無關組 ,如果這個不分組本身是線性無關的,並且從這向量組中任意添一向量(如果還有的話),所得的部分向量都線性相關。
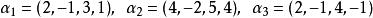 最大線性無關組
最大線性無關組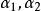 最大線性無關組
最大線性無關組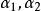 最大線性無關組
最大線性無關組例如,在向量組 中,由 組成的部分組就是一個極大線性無關組。首先, 線性無關,因為由
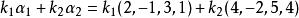 最大線性無關組
最大線性無關組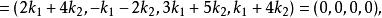 最大線性無關組
最大線性無關組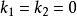 最大線性無關組
最大線性無關組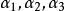 最大線性無關組
最大線性無關組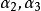 最大線性無關組
最大線性無關組就有 。同時我們知道, 線性相關。不難看出, 也是一個極大線性無關組。
應該看到,一個線性無關向量組的極大線性無關組就是這個向量組本身。
極大線性無關組的一個基本性質是,任意一個極大線性無關組都與向量組本身等價。
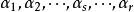 最大線性無關組
最大線性無關組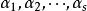 最大線性無關組
最大線性無關組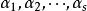 最大線性無關組
最大線性無關組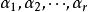 最大線性無關組
最大線性無關組事實上,設向量組 ,而 是它的一個極大線性無關組。所謂等價就是它們可以互相線性表出。因為 是 的一部分,當然可以被這個向量組線性表出,即
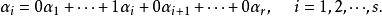 最大線性無關組
最大線性無關組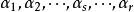 最大線性無關組
最大線性無關組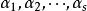 最大線性無關組
最大線性無關組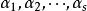 最大線性無關組
最大線性無關組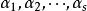 最大線性無關組
最大線性無關組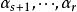 最大線性無關組
最大線性無關組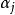 最大線性無關組
最大線性無關組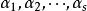 最大線性無關組
最大線性無關組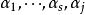 最大線性無關組
最大線性無關組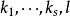 最大線性無關組
最大線性無關組因此,問題在於 是否可以被 線性表出。向量 中每一個都可以被 線性表出是顯然的。再來看 中的向量,設 是這樣一個向量,由極大線性無關組 的極大性,向量組 線性相關,也就是說,有不全為零的數 使得
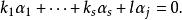 最大線性無關組
最大線性無關組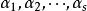 最大線性無關組
最大線性無關組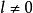 最大線性無關組
最大線性無關組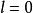 最大線性無關組
最大線性無關組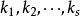 最大線性無關組
最大線性無關組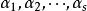 最大線性無關組
最大線性無關組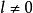 最大線性無關組
最大線性無關組因為 是線性無關的,可證必有 。否則,設 ,那么 就不全為零,於是 線性相關,這與假設矛盾。由 ,上式可以改寫為
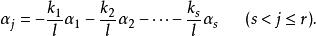 最大線性無關組
最大線性無關組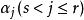 最大線性無關組
最大線性無關組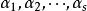 最大線性無關組
最大線性無關組這就是說, 可以被 線性表出。於是證明了向量組與它的極大線性無關組的等價性。
由上面的例子可以看出,向量組的極大線性無關組不是惟一的。但是每一個極大線性無關組都與向量組本身等價,因而,一向量組的任意兩個極大線性無關組都是等價的。
定理1
一向量組的極大線性無關組都含有相同個數的向量。
定理1表明,極大線性無關組所含向量的個數與極大線性無關組的選擇無關,它直接反映了向量組本身的性質。
定義4
向量組的極大線性無關組所含向量的個數稱為這個向量組的秩。
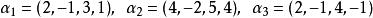 最大線性無關組
最大線性無關組例如,向量組的秩就是2。
因為線性無關的向量組就是它自身的極大線性無關組,所以一向量組線性無關的充分必要條件為它的秩與它所含向量的個數相同。
我們知道,每一向量組都與它的極大線性無關組等價。由等價的傳遞性可知,任意兩個等價向量組的極大線性無關組也等價。所以,等價的向量組必有相同的秩。
還要指出:含有非零向量的向量組一定有極大線性無關組,且任一個無關的部分向量組都能擴充成一個極大線性無關組。全部由零向量組成的向量組沒有極大線性無關組,規定這樣的向量組的秩為零。
