概述
科技名詞定義中文名稱：結構最佳化設計；
定義：工程結構在滿足約束條件下按預定目標求出最優方案的設計方法；
套用學科：水利科技（一級學科）；工程力學、工程結構、建築材料（二級學科）；工程結構（水利）（三級學科）；
以上內容由全國科學技術名詞審定委員會審定公布。
傳統的結構最佳化設計，實際上指的是結構分析，其過程大致是假設-分析-校核-重新設計。重新設計的目的也是要選擇一個合理的方案，但它只屬分析的範疇；且只能憑設計者的經驗作很少幾次重複以通過“校核”為滿足。結構最佳化指的是結構綜合，其過程大致可歸納為：假定-分析-搜尋-最優設計四個階段。其中的搜尋過程是修改並最佳化的過程。它首先判斷設計方案是否達到最優（包括滿足各種給定的條件），如若不是，則按某種規則進行修改，以求逐步達到預定的最優指標。
發展簡史
結構最佳化設計的構想由來已久。J．C．麥克斯韋於1854年和J．H．米歇爾於1905年就曾研究過在不加任何形狀約束條件下桁架式結構的最優布局問題。他們的工作在理論上有一定意義，但所得結果往往在工藝上無法實現。到20世紀40年代，在航空結構的構件設計中提出了所謂“同步極限”準則，即認為一個構件的最優設計，應使它在受力後各部分都同時達到極限狀態。求解方法一般採用經典的受等式約束的函式極小化理論。但是這種方法只能處理一些簡單的問題，例如，處理形狀簡單的薄壁結構部件的最佳化問題。此外，還曾提出滿應力設計準則，即認為最優結構的每一部件的應力應在至少一種工況下達到它的容許限值。對於靜定結構，這個滿應力準則是不難實現的，但是對於靜不定結構，滿應力設計需要經過多次的反覆分析和修改才能完成，在還沒有電子計算機的時代，這是很難實現的。60年代初，出現了現代化的結構最佳化設計理論和方法，它是以利用電子計算機為基礎的。
數學模型
輕鋼結構設計的最終目的是要給出一個經濟合理的設計方案。最佳化設計方法，能較好地適應這方面的要求。輕鋼結構採用最佳化設計，對於減輕結構重量、降低用鋼量和結構造價有著明顯的意義。目前國內對輕鋼結構的最佳化設計已進行了一些研究和套用，編制了相應的計算程式，利用計算機實現了對截面的自動優選以求得重量最小、用料最省或造價最低的設計方案。這對於提高輕鋼結構的設計質量，加快設計進程都起了一定的作用。下面針對輕鋼結構建立其最佳化設計的數學模型。
1．設計變數
輕鋼結構的主要幾何參數如跨度、檐口高、屋面坡度、縱向柱間距等通常由業主或建築師確定。可供最佳化的變數主要是截面參數。具體說，就是各工字鋼截面的翼緣寬、厚，腹板的高、厚等。鋼板的厚度是離散變數，而腹板和翼緣的高（寬）一般也是從一系列有規律的數中選取，因此輕鋼結構的設計變數通常是離散變數。
2．目標函式
結構重量是輕鋼結構最佳化設計的重要指標，且比較容易寫成設計變數的函式形式，故輕鋼結構通常以用鋼量最少為最佳化目標。
3．約束條件
輕鋼結構最佳化設計必須滿足以下約束條件：
（1）強度、穩定約束條件。
輕鋼結構構件必須滿足強度和穩定要求。
（2）剛度約束條件。
輕鋼結構的構件尺寸在最佳化時，結構的整體剛度必須滿足變形控制要求。具體說，就是橫樑的最大垂直位移、柱頂的最大水平位移、吊車軌頂處的最大水平位移等必須滿足有關規範規定的變形控制值。
（3）截面尺寸約束條件。
輕鋼結構截面尺寸的選擇必須滿足有關規範的構造要求和使用要求，如所有截面的腹板高度必須大於翼緣寬度，所有截面的翼緣厚度必須比腹板厚度大2mm以上等。
（4）結構整體約束條件。
輕鋼結構的最佳化設計必須滿足結構整體約束條件，即構件截面尺寸的選擇必須要保證梁、柱截面的連續性以及合理性，滿足常規的加工和使用要求等。
（5）變數的上、下限約束條件。
基本方法
結構最佳化設計有兩個主要方法：數學規劃法和最佳化準則法：
教學規劃法
數學規劃法的命題是：求n個變數x(i=l，2，…，n)，滿足m個約束條件G(x)≤0 (j=l，2，…，m)，且使目標函式W(x)為最小(或最大)。如果約束條件和目標函式都是x的線性函式，這便是線性規劃問題，已有成熟的解法；如果在這些函式中有一個是非線性函式，便成為非線性規劃問題。隨著非線性函式的性質和形式的不同，非線性規劃問題有很多類型，特殊的解法很多，在套用上各有局限性，沒有普遍適用的最好解法。
用數學規劃法來作結構最佳化設計，變數x便代表可以變化的各種結構參數，如元件截面積或厚度、節點位置、材料性質等；約束條件G(x)≤0代表設計必須滿足的各種限制，例如結構各部位的靜應力，動應力或變位不得超過規定的容許值，元件的截面或厚度尺寸不得超出給定的範圍，結構的頻率不應落在某個禁區，結構的失穩臨界力或飛行器的顫振速度不得小於某一下限，等等；而目標函式則代表結構最佳化所追求的指標，例如，結構重量最小和成本最低等可以定量的指標；也可將重量、造價作為約束條件，而把某種結構性能，例如剛度作為目標函式。
數學規劃法的基本目的是，在以設計變數為坐標的多維空間裡搜尋最優點。如果有n個設計變數，則相應的n維設計變數空間中的每個點都代表一個設計方案。在無限多的點中要儘快地搜尋出既滿足所有的約束條件，又能使目標函式儘量接近最小值(或最大值)的點，就是數學規劃設計法的任務，這種搜尋的過程稱為“最佳化過程”。
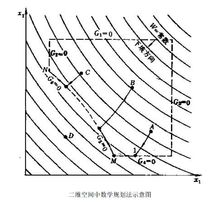結構最佳化設計附圖表示一個二維設計空間，圖中的一簇曲線是目標函式W(x1，x2)為常數的等值線。約束函式Gj(x1，x2)為零的曲線所圍成的區域是可行域。A、B、C點各代表一個可行的方案.圍線以外的點(如D)不滿足約束條件，所以是不可行方案。顯然，滿足約束條件並使目標函式W最小的最優方案點是M。數學規劃就是要以最迅速的方式找到點M。這好比在山坡上—個用柵欄圍起來的區域裡找最低點，如果這個山坡不是凹的，則可以斷定最低點必在柵欄所在的邊界上。數學規劃提供了很多搜尋的辦法，基本原則都是在選好一個出發點後，經過分析判斷，找出一個邁步的有利方向，沿這個方向跨出有利的步長以到達新的一點。再從此點出發，重複上述過程，一步一步走下去，直到再也找不到可走的有利方向，就是達到了最低點。從第n點到第(n+1)點這一步可表達為：
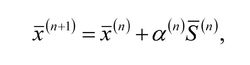結構最佳化設計
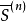結構最佳化設計式中
為有利方向，
為有利步長係數，它們依靠在點進行的分析所提供的信息來確定。例如，從可行點A出發，沿著等高線的梯度負向，即最陡下降方向逐步走到邊界點1，然後再沿著邊界逐步走到最低點M，這個方法叫作梯度投影法。實際上還有很多其他的方法。可以看出，如果初始出發點選的是B，用同樣的走法也可以走到最低點M；但如果初始點選的是C，那就會走到另一個局部最低點N。M點代表全局最優解，因為它是全部可行域中的最低點。N點只是在它附近的可行域中的最低點，所以是局部最優解。現在還沒有一個可靠的實用方法能保證搜尋到的解一定是全局最優解。一般是在可能的情況下取若干不同的出發點作幾次搜尋，以期找到全局最優解。
如果是線性規劃問題，搜尋過程就簡便得多。所以有時把非線性問題轉化成一系列線性問題來逼近。為此，在某一設計點附近將目標函式和約束函式都線性化，也就是在該點將函式作泰勒展開，並只保留它們的線性項。然後作有一定步長限制的線性規劃，得到新的一點。如此重複下去，直到收斂於最優點為止。
由於不帶約束的規劃問題比較容易作，所以有時也把有約束問題轉化成一個序列的無約束問題。為此，可以把約束表示成一個罰函式加到目標函式上去，構成一個新的目標函式，即
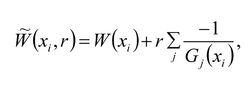結構最佳化設計
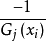結構最佳化設計式中
即為罰函式，r是個相當小的正數，它在序列無約束問題中，逐次減小。因為r值很小，當代表某一設計方案的點在離開邊界較遠的可行域內部行動時，;但是當接近可行域的邊界．某約束函式Gj(xi)將由負值趨近於零，於是罰函式急劇增大，因此，的最小點不可能越過可行域邊界。r越小，無約束問題的W最小點越接近於有約束問題的W最小點。但是如果一開始就取很小的r，無約束問題將遇到收斂上的困難，所以有必要將有約束問題化成一個序列的無約束問題，讓係數r在這個序列中逐漸減小到適當的程度。
此外，還有一些非線性規劃的特殊方法，如幾何規劃和動態規劃，各有其適應的範圍，在結構最佳化設計中也得到套用。
最佳化準則法
以滿足某種準則來代替目標函式在約束條件下取極值的方法，叫作最佳化準則法。最簡單的一個最佳化準則法，便是前面提到的滿應力設計方法。只有對於內力分布不隨設計變數改變而變化的靜定結構，而且容許應力與設計變數無關的情況下，才能通過一次結構分析和修改設計得出滿應力結構。對於其他情況，為使各元件趨向於滿應力，必須進行下列的選代：
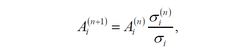結構最佳化設計
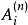結構最佳化設計式中
和
為第n次疊代的第i元件的截面積和最大應力，
為第i元件的容許應力。公式給出經過修正的第i元件的截面積
。疊代收斂時，
，就達到
的滿應力準則。滿應力準則和結構最小重量之間沒有必然的聯繫，但是一般的滿應力設計可能相當接近於甚至就等於最輕設計。當然，這個方法只適用於受應力約束的最輕設計問題。
60年代末，出現了更科學的最佳化準則法。它通過數學推演，把在一定約束下求最輕設計化為求滿足某種最佳化準則的設計，舉只有一個變位約束最佳化設計問題為例：求xi，滿足在單約束G(xi)≤0的條件下，使W(xi)最小(i=1，2，…，n)。可以用目標函式和約束函式建立一個新的混合函式，即拉格朗日函式：
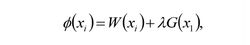結構最佳化設計式中λ為一個待定的拉格朗日乘子。原來的約束極值問題等價於：
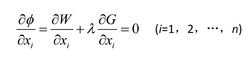結構最佳化設計由此得：
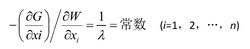結構最佳化設計
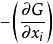結構最佳化設計這便是關於單約束最佳化設計必須滿足的準則。最佳化設計x，必須使最佳化函式和目標函式對任一個設計變數xi的偏導數的比值是同一個常數。如果約束函式G是某處的變位，則
表示設計變數xi作單位增長時變位值的減小，即結構的剛度收益；如果目標函式W是結構的總重量，則
表示xi作單位增長時重量的增加，即付出的代價。因此，上述準則可以理解為：最輕設計必須滿足的條件是：當任何一個自由設計變數作單位變化時，結構的剛度收益和重量支出的比值應彼此相等，即都等於某一常數。也可以說，在最輕結構中，自由設計變數都被調整到具有相等的最佳化效率。這意味著對結構剛度貢獻大的設計變數，應該多負點重量。用這個準則，可以建立一套疊代算法，從某個初始方案開始，用選代方法逐步使這個準則得到滿足，最後獲得最佳化方案。如果是多約束問題，約束不止一個，最佳化準則便是：
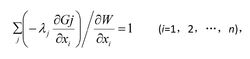結構最佳化設計式中λj是對應於第j個有效約束Gi的拉格朗日乘子，可以理解為:
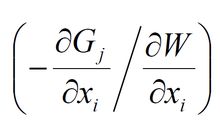結構最佳化設計的權係數。所有λj都應為非負值，即λj≥0；如果由準則算出的某λj為負值，則相應的約束就是不起作用的松約束，應該取這個λj為零值。多約束的算法，要比單約束複雜，其困難在於每一步選代都要區別出起作用的和不起作用的約束。
最佳化準則法自60年代末以來被成功地用於航空結構設計。它的優點是算法簡單，收斂快，不受變數多少的影響。一般經過十次左右的疊代，就可滿足設計要求。選代次數的多少，在實際的結構最佳化設計中極為重要。因為選代一次，就需要將結構重新分析一次，而作一次結構分析的代價是很大的。
套用和展望
計算機化的結構最佳化設計，首先在航空工業中得到重視和套用，後又逐漸推廣到建築，造船、機械製造等領域。二十年來的發展證明，教學規劃法和最佳化準則法是兩個行之有效的方法，但各有利弊。前者通過與力學概念的緊密結合，可減少結構分析的次數，從而減少計算工作量。後者則正在改進它的適應性，以便擴大套用範圍。在實際套用中，這兩種方法常常互相取長補短，配合使用。
結構最佳化設計只是工程系統設計中的—個環節，結構的最佳化應包括在大系統的最佳化之中。即使是只考慮結構本身的最佳化，也要經歷許多層次。層次越高，在最佳化中可變參數的性質越廣，不僅結構截面參數可變，結構的幾何形狀、組合方式以至各部分材料也是可變的。今後要努力的方向是擴大最佳化範圍和提高最佳化效益。
參考書目
R．H．Gallagher and O．C．ZienkieWicz，ed.， OptimumStructural Design，Theory and Applications，John Wiley&Sons，London，1973．
錢令希著：《工程結構最佳化設計》，水利電力出版社，北京，1983。
《1980年全國計算力學會議文集》，北京大學出版社，北京，198l。
