定義
如果一個函式,它的範圍(值域)是在實數範圍內的,那么就稱它為實函式,也可以叫實值函式。
A function whose range is in the real numbers is said to be a real function.
函式
[function]
 實值函式
實值函式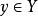 實值函式
實值函式 實值函式
實值函式 實值函式
實值函式 實值函式
實值函式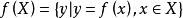 實值函式
實值函式函式即映射,設 X 與 Y 為給定的兩個集合,f 是某個法則,每個按照 f 對應唯一的,稱 f 為的一個函式(映射)。x 通過 法則 f 對應的 y 值記為,x 稱為 自變數(independent variable),y 稱為因變數。亦稱“函式”或“ y 是 x 的函式“。X 稱為定義域;稱為值域。
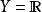 實值函式
實值函式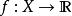 實值函式
實值函式 實值函式
實值函式當時,函式稱為 實值函式。特別地,當 X,Y 均為實數集時,函式稱為 一元函式或 一元實函式。
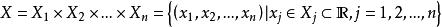 實值函式
實值函式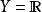 實值函式
實值函式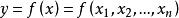 實值函式
實值函式當,時,函式是自變數,y 是因變數。
套用
函式是數學的一個基本概念,其概念的形成有較長的歷史過程。在古代數學中函式依賴的思想沒有明顯地表達出來,而且不是獨立的研究對象。函式概念的雛形在中世紀開始出現於學者的著作中。
但僅僅在17 世紀,首先在費馬、笛卡兒、牛頓、萊布尼茨的工作中,函式才作為一個獨立的概念逐漸定形。函式一詞最先出現在萊布尼茨的著作中,用以表示隨曲線上的點變動的量。
1718 年,約翰第一,伯努利(J.Bernoulli I) 定義函式為“由變數與常量以任何適當方式構成的量”。
1755 年,歐拉在《微分學) 中給出更一般的定義,即函式都能用解析式表示,這也是當時數學家普遍的看法。
直到1807 年,傅立葉用三角級數表示更一般的函式後,函式才與其表達方式逐漸分離。
1837 年,狄利克雷用對應的觀點給出了區間上的明確的函式定義,無須函式有解析表達式。狄利克雷的定義沿用至今,有重要的影響。
函式即映射的定義由戴德金(R.Dedekind) 於1887 年給出。
函式的概念極其廣泛。例如,在公理化體系的機率定義中,機率實際上是一種定義在事件城上滿足3 三條公設的函式。

