基本定義
最最佳化方法書籍最最佳化方法(也稱做運籌學方法)是近幾十年形成的，它主要運用數學方法研究各種系統的最佳化途徑及方案，為決策者提供科學決策的依據。最最佳化方法的主要研究對象是各種有組織系統的管理問題及其生產經營活動。最最佳化方法的目的在於針對所研究的系統，求得一個合理運用人力、物力和財力的最佳方案，發揮和提高系統的效能及效益，最終達到系統的最優目標。實踐表明，隨著科學技術的日益進步和生產經營的日益發展，最最佳化方法已成為現代管理科學的重要理論基礎和不可缺少的方法，被人們廣泛地套用到公共管理、經濟管理、工程建設、國防等各個領域，發揮著越來越重要的作用。本章將介紹最最佳化方法的研究對象、特點，以及最最佳化方法模型的建立和模型的分析、求解、套用。主要是線性規劃問題的模型、求解(線性規劃問題的單純形解法)及其套用――運輸問題;以及動態規劃的模型、求解、套用――資源分配問題。
最最佳化方法
1.微分學中求極值
2.無約束最最佳化問題
3.常用微分公式
4.凸集與凸函式
5.等式約束最最佳化問題
6.不等式約束最最佳化問題
7.變分學中求極值
詳細資訊
數學意義
為了達到最最佳化目的所提出的各種求解方法。從數學意義上說，最最佳化方法是一種求極值的方法，即在一組約束為等式或不等式的條件下，使系統的目標函式達到極值，即最大值或最小值。從經濟意義上說，是在一定的人力、物力和財力資源條件下，使經濟效果達到最大(如產值、利潤)，或者在完成規定的生產或經濟任務下，使投入的人力、物力和財力等資源為最少。
發展簡史
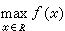黃金分割比公元前 500年古希臘在討論建築美學中就已發現了長方形長與寬的最佳比例為1.618,稱為黃金分割比。其倒數至今在優選法中仍得到廣泛套用。在微積分出現以前，已有許多學者開始研究用數學方法解決最最佳化問題。例如阿基米德證明:給定周長，圓所包圍的面積為最大。這就是歐洲古代城堡幾乎都建成圓形的原因。但是最最佳化方法真正形成為科學方法則在17世紀以後。17世紀，I.牛頓和G.W.萊布尼茨在他們所創建的微積分中，提出求解具有多個自變數的實值函式的最大值和最小值的方法。以後又進一步討論具有未知函式的函式極值，從而形成變分法。這一時期的最最佳化方法可以稱為古典最最佳化方法。第二次世界大戰前後，由於軍事上的需要和科學技術和生產的迅速發展，許多實際的最最佳化問題已經無法用古典方法來解決，這就促進了近代最最佳化方法的產生。近代最最佳化方法的形成和發展過程中最重要的事件有: 以蘇聯Л.В.康托羅維奇和美國G.B.丹齊克為代表的線性規劃;以美國庫恩和塔克爾為代表的非線性規劃;以美國R.貝爾曼為代表的動態規劃;以蘇聯Л.С.龐特里亞金為代表的極大值原理等。這些方法後來都形成體系，成為近代很活躍的學科，對促進運籌學、管理科學、控制論和系統工程等學科的發展起了重要作用。
工作步驟
用最最佳化方法解決實際問題，一般可經過下列步驟:①提出最最佳化問題，收集有關數據和資料;②建立最最佳化問題的數學模型,確定變數,列出目標函式和約束條件;③分析模型，選擇合適的最最佳化方法;④求解，一般通過編製程序，用計算機求最優解;⑤最優解的檢驗和實施。上述 5個步驟中的工作相互支持和相互制約，在實踐中常常是反覆交叉進行。
模型的基本要素
最最佳化模型一般包括變數、約束條件和目標函式三要素:①變數:指最最佳化問題中待確定的某些量。變數可用x=(x1，x2,…,xn)T表示。②約束條件:指在求最優解時對變數的某些限制,包括技術上的約束、資源上的約束和時間上的約束等。列出的約束條件越接近實際系統，則所求得的系統最優解也就越接近實際最優解。約束條件可用 gi(x)≤0表示i=1,2，…，m，m 表示約束條件數;或x∈R(R表示可行集合)。③目標函式:最最佳化有一定的評價標準。目標函式就是這種標準的數學描述，一般可用f(x)來表示，即f(x)=f(x1，x2,…,xn)。要求目標函式為最大時可寫成;要求最小時則可寫成。目標函式可以是系統功能的函式或費用的函式。它必須在滿足規定的約束條件下達到最大或最小。 問題的分類 最最佳化問題根據其中的變數、約束、目標、問題性質、時間因素和函式關係等不同情況，可分成多種類型(見表)。最最佳化方法
最最佳化方法
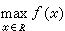最最佳化方法不同類型的最最佳化問題可以有不同的最最佳化方法，即使同一類型的問題也可有多種最最佳化方法。反之,某些最最佳化方法可適用於不同類型的模型。最最佳化問題的求解方法一般可以分成解析法、直接法、數值計算法和其他方法。①解析法:這種方法只適用於目標函式和約束條件有明顯的解析表達式的情況。求解方法是:先求出最優的必要條件，得到一組方程或不等式，再求解這組方程或不等式，一般是用求導數的方法或變分法求出必要條件，通過必要條件將問題簡化，因此也稱間接法。②直接法:當目標函式較為複雜或者不能用變數顯函式描述時，無法用解析法求必要條件。此時可採用直接搜尋的方法經過若干次疊代搜尋到最優點。這種方法常常根據經驗或通過試驗得到所需結果。對於一維搜尋(單變數極值問題)，主要用消去法或多項式插值法;對於多維搜尋問題(多變數極值問題)主要套用爬山法。③數值計算法:這種方法也是一種直接法。它以梯度法為基礎，所以是一種解析與數值計算相結合的方法。④其他方法:如網路最最佳化方法等(見網路理論)。
解析性質
根據函式的解析性質，還可以對各種方法作進一步分類。例如，如果目標函式和約束條件都是線性的，就形成線性規劃。線性規劃有專門的解法，諸如單純形法、解乘數法、橢球法和卡馬卡法等。當目標或約束中有一非線性函式時,就形成非線性規劃。當目標是二次的,而約束是線性時，則稱為二次規劃。二次規劃的理論和方法都較成熟。如果目標函式具有一些函式的平方和的形式，則有專門求解平方和問題的最佳化方法。目標函式具有多項式形式時，可形成一類幾何規劃。
最優解的概念
最最佳化問題的解一般稱為最優解。如果只考察約束集合中某一局部範圍內的優劣情況，則解稱為局部最優解。如果是考察整個約束集合中的情況，則解稱為總體最優解。對於不同最佳化問題，最優解有不同的含意，因而還有專用的名稱。例如，在對策論和數理經濟模型中稱為平衡解;在控制問題中稱為最優控制或極值控制;在多目標決策問題中稱為非劣解(又稱帕雷托最優解或有效解)。在解決實際問題時情況錯綜複雜，有時這種理想的最優解不易求得，或者需要付出較大的代價，因而對解只要求能滿足一定限度範圍內的條件,不一定過分強調最優。50年代初,在運籌學發展的早期就有人提出次最佳化的概念及其相應的次優解。提出這些概念的背景是:最最佳化模型的建立本身就只是一種近似，因為實際問題中存在的某些因素，尤其是一些非定量因素很難在一個模型中全部加以考慮。另一方面，還缺乏一些求解較為複雜模型的有效方法。1961年H.A.西蒙進一步提出滿意解的概念，即只要決策者對解滿意即可。
最最佳化方法的套用
最最佳化一般可以分為最優設計、最優計畫、最優管理和最優控制等四個方面。①最優設計:世界各國工程技術界,尤其是飛機、造船、機械、建築等部門都已廣泛套用最最佳化方法於設計中，從各種設計參數的優選到最佳結構形狀的選取等，結合有限元方法已使許多設計最佳化問題得到解決。一個新的發展動向是最優設計和計算機輔助設計相結合。電子線路的最優設計是另一個套用最最佳化方法的重要領域。配方配比的優選方面在化工、橡膠、塑膠等工業部門都得到成功的套用,並向計算機輔助搜尋最佳配方、配比方向發展(見優選法)。②最優計畫:現代國民經濟或部門經濟的計畫，直至企業的發展規劃和年度生產計畫，尤其是農業規劃、種植計畫、能源規劃和其他資源、環境和生態規劃的制訂,都已開始套用最最佳化方法。一個重要的發展趨勢是幫助領導部門進行各種最佳化決策。③最優管理:一般在日常生產計畫的制訂、調度和運行中都可套用最最佳化方法。隨著管理信息系統和決策支持系統的建立和使用，使最優管理得到迅速的發展。④最優控制:主要用於對各種控制系統的最佳化。例如，飛彈系統的最優控制，能保證用最少燃料完成飛行任務,用最短時間達到目標;再如飛機、船舶、電力系統等的最優控制，化工、冶金等工廠的最佳工況的控制。計算機接口裝置不斷完善和最佳化方法的進一步發展，還為計算機線上生產控制創造了有利條件。最優控制的對象也將從對機械、電氣、化工等硬系統的控制轉向對生態、環境以至社會經濟系統的控制。
圖書信息
書 名: 最最佳化方法
作 者:張立衛
出版社:科學出版社
出版時間: 2010年6月1日
ISBN: 9787030276490
開本: 16開
最最佳化方法定價: 27.00元
內容簡介
《最最佳化方法》介紹最最佳化模型的理論與計算方法，其中理論包括對偶理論、非線性規劃的最優性理論、非線性半定規劃的最優性理論、非線性二階錐最佳化的最優性理論；計算方法包括無約束最佳化的線搜尋方法、線性規劃的單純形方法和內點方法、非線性規劃的序列二次規劃方法、非線性規劃的增廣Lagrange方法、非線性半定規劃的增廣Lagrange方法、非線性二階錐最佳化的增廣Lagrange方法以及整數規劃的Lagrange鬆弛方法。《最最佳化方法》注重知識的準確性、系統性和算法論述的完整性，是學習最最佳化方法的一本入門書。
《最最佳化方法》可用作高等院校數學系高年級本科生和管理專業研究生的教材，也可作為相關工程技術人員的參考用書。
圖書目錄
前言
第1章 變分分析的相關素材
1.1 凸分析素材
1.1.1 凸集合
1.1.2 凸函式的閉包
1.1.3 共軛函式
1.1.4 次可微性
1.2 集值映射的極限
1.3 方嚮導數
1.4 集合的切錐與二階切集
1.4.1 集合的切錐
1.4.2 二階切集
1.4.3 函式水平集的切錐與二階切集
1.4.4 負卦限錐的切錐與二階切集
1.5 有限維系統的穩定性
1.5.1線性系統
1.5.2 集契約束的線性系統
1.5.3 集契約束的非線性系統
第2章 無約束最佳化
2.1 引言
2.2 線搜尋方法
2.2.1 線搜尋原則
2.2.2 下降方法的收斂性
2.3 最速下降方法
2.3.1 最速下降方法的全局收斂性
2.3.2 最速下降方法的收斂速度
2.4 Newton法
2.4.1 經典Newton法
2.4.2 帶線搜尋的：Newton法
2.4.3 自協調函式的Newton法
2.5 擬Newton法
2.5.1 擬Newton方程和著名的擬Newton公式
2.5.2 擬Newton法求解凸二次規劃
2.5.3 Dixon定理
2.5.4 DFP方法的收斂性
2.5.5 BFGS方法的收斂性
2.5.6 限制Broyden類方法的收斂性
2.6 共軛梯度方法
2.6.1 共軛方向
2.6.2 共軛梯度方法求解二次規劃
2.6.3 求解無約束最佳化問題的FR方法
2.7 信賴域方法
2.7.1 信賴域基本算法
2.7.2 Cauchy點與模型下降
2.7.3 信賴域算法的收斂性
第3章 線性規劃
3.1 線性規劃問題及其性質
3.2 單純形法
3.3 Bland原則
3.4 線性規劃的對偶定理
3.5 對偶單純形方法
3.6 線性規劃的Karmakar內點法
3.6.1 解析中心與勢函式
3.6.2 線性規劃的勢函式
3.6.3 線性規劃的中心路徑
3.6.4 線性規劃的Karmarkar算法
第4章 對偶理論
4.1 共軛對偶性
4.2 Lagrange對偶性
4.3 對偶理論的套用
第5章 最優性條件
5.1 一階最優性條件
5.2 廣義Lagrange乘子
5.3 二階最優性條件
第6章 增廣Lagrange函式方法
6.1 懲罰與障礙函式方法
6.1.1 懲罰函式方法
6.1.2 經典障礙函式方法
6.2 增廣Lagrange函式方法
6.2.1 增廣Lagrange函式
6.2.2 Bertsekas的經典結果
6.2.3 對偶收斂率
第7章 序列二次規劃（SQP）方法
7.1 等式約束最佳化問題的局部方法
7.1.1 Newton法
7.1.2 KKT系統
7.1.3 既約Hesse陣方法
7.2 一般約束最佳化問題的局部方法
7.2.1 序列二次規劃方法
7.2.2 原始.對偶二次收斂性
7.2.3 原始超線性收斂性
7.3 線搜尋全局方法
7.3.1 不可微懲罰函式
7.3.2 線搜尋SQP方法
7.3.3 Maratos效應
參考文獻
