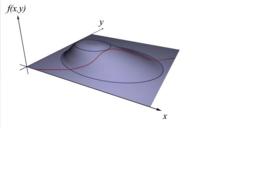
定義
對於具有l個等式約束的n維最佳化問題
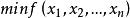拉格朗日乘子法
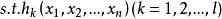拉格朗日乘子法,
拉格朗日乘子法把原目標函式 改造成為如下形式的新的目標函式
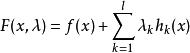拉格朗日乘子法
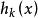拉格朗日乘子法 拉格朗日乘子法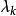
拉格朗日乘子法式中的 就是原目標函式 的等式約束條件，而待定係數 稱為 拉格朗日乘子。這種方法稱為 拉格朗日乘子法。
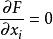拉格朗日乘子法
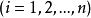拉格朗日乘子法
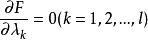拉格朗日乘子法在極值點處，有 和 ，共有n+l個方程，足以算出這n+l個變數，此法也稱為 升維法。
基本原理
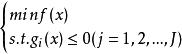拉格朗日乘子法拉格朗日乘子法是一種經典的求解條件極值的解析方法，可將所有約束的最佳化模型問題轉化為無約束極值問題的求解。一般帶不等式約束的最最佳化問題求解如下式：
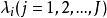拉格朗日乘子法
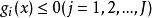拉格朗日乘子法
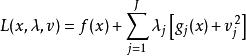拉格朗日乘子法
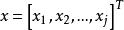拉格朗日乘子法
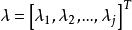拉格朗日乘子法
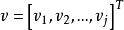拉格朗日乘子法拉格朗日乘子法是用於變數無關的是常數 分別乘各約束函式 並與目標函式相加得到如下的拉格朗日函式： ，式中： 為自變數； 為拉格朗日乘子量； 為鬆弛變數。
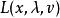拉格朗日乘子法
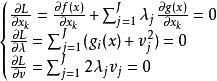拉格朗日乘子法
拉格朗日乘子法 拉格朗日乘子法則 在 處取極值的必要條件為： ，依據上式求得 即為最優解。
計算過程
1.假設需要求極值的目標函式(objective function)為f(x,y)，限制條件為φ(x,y)=M
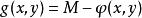拉格朗日乘子法2.設
3.定義一個新函式
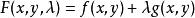拉格朗日乘子法4.用偏導數方法列出方程：
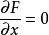拉格朗日乘子法
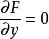拉格朗日乘子法
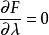拉格朗日乘子法5.求出x,y,λ的值，代入即可得到目標函式的極值
關鍵參數含義
拉格朗日乘子法（1） 是由參數M所引起的約束條件變化時，對目標函式最優值影響的度量；或者說表示了最優值的“靈敏度”。
（2）當約束條件M增加一個單位時，目標函式值f將近單位。
拉格朗日乘子法（3）在經濟學上參數 表示產品或資源M增加一個單位時，所帶來的最大社會效益f，常稱為“邊際效益”或“臨界值”，在商業經營決策中很有用處。
直觀意義
引理一
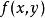拉格朗日乘子法
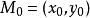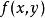拉格朗日乘子法 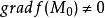拉格朗日乘子法
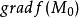拉格朗日乘子法
拉格朗日乘子法
拉格朗日乘子法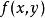 拉格朗日乘子法如果函式 是光滑的，並且 是 的一個正則點（即 ），那么， 垂直於過 的 的等值線。
引理二
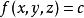拉格朗日乘子法
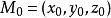拉格朗日乘子法 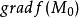拉格朗日乘子法在等值面 上的每個正則點 ，向量 垂直於等值面，並且這個向量是唯一 的（不計其某一常數倍）。
定理
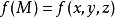拉格朗日乘子法
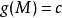拉格朗日乘子法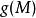 拉格朗日乘子法 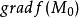拉格朗日乘子法
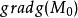拉格朗日乘子法 拉格朗日乘子法
拉格朗日乘子法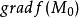 拉格朗日乘子法 拉格朗日乘子法 拉格朗日乘子法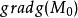 拉格朗日乘子法假設 在曲面S: 上的點 有最大（小）值，並且 不是 的臨界點（g的三個偏導數都等於零的點叫g的臨界點），則 平行於 ，即存在某個常數 ，使 = 。
部分套用
在條件最值中的套用
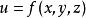拉格朗日乘子法
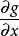拉格朗日乘子法
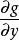拉格朗日乘子法
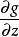拉格朗日乘子法
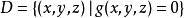拉格朗日乘子法設 的最值存在，且 ， ， 在 上時不同時為零，則最值點必是極值點，從而必是Lagrange函式的駐點。
在不等式證明中的套用
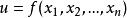拉格朗日乘子法
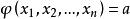拉格朗日乘子法
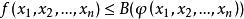拉格朗日乘子法設 在條件 之下的最大值為B(a)，則 。
在求隱函式極值中的套用
實際用途
假設目標函式代表一個工廠生產產品的數量，約束條件限制了生產中投入的原料和人力的總成本，我們求目標函式的極值，就是要求在成本一定的條件下，如何分配利用人力和原料，從而使得生產量達到最大。此時λ便代表，當成本條件改變時，工廠可達到的生產量最大值的變化率。
