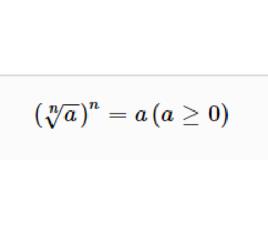基本概念
正實數的n次算術根是這個實數的正的n次方根;零的n次算術根是零;負實數沒有算術根。
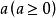 算術根
算術根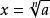 算術根
算術根n次冪等於的非負實數叫做a的n次 算術方根。
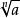 算術根
算術根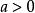 算術根
算術根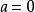 算術根
算術根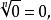 算術根
算術根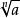 算術根
算術根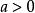 算術根
算術根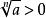 算術根
算術根正數a的正的n次方根叫做a的n次 算術方根,簡稱 算術根.算術根常用表示;其中,當,因此用符號表示的總是 非負數,特別的,時,。一般的,
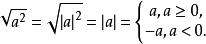 算術根
算術根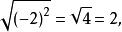 算術根
算術根如但不能等於-2。
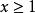 算術根
算術根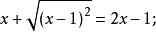 算術根
算術根又如,時,
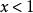 算術根
算術根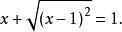 算術根
算術根時,
n次方根
n次方根的定義
以下談到數時,都是指在 實數的範圍內。
如果:
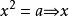 算術根
算術根 算術根
算術根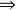 算術根
算術根叫的 平方根(代表由前面可以推出或得到後面的結論)
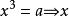 算術根
算術根 算術根
算術根叫的 立方根。
推而廣之,容易得到n次(n≥2的整數)方根的定義。
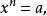 算術根
算術根如果則x叫做a的 n次方根,求a的n次方根的運算叫 把a開n次方。a稱為 被開方數,n稱為 根指數(n≥2的整數)。
這樣, 開方是乘方的一種逆運算。
偶次方根的性質
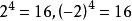 算術根
算術根,而2與-2以外的任何實數的四次方都不等於16。2是16的正的四次方根記為:
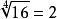 算術根
算術根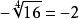 算術根
算術根(這樣,)
一般的正的實數的偶次方根有兩個,它們互為相反的數。
負數沒有偶次方根,零的偶次方根為零。
奇次方根的性質
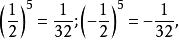 算術根
算術根 算術根
算術根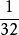 算術根
算術根 算術根
算術根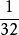 算術根
算術根而以外的任何實數的五次方,都不等於,是的(唯一)五次方根,記為:
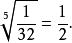 算術根
算術根同樣,
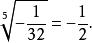 算術根
算術根一般,任意實數都有唯一的奇次方根,正數的奇次方根為正數,負數的奇次方根為負數,而零的奇次方根為零。
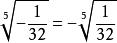 算術根
算術根由上例,我們有,結論是,一切實數如果有某一n次(n≥2的整數)方根的話,它必然可以用一個非負的數的唯一正方根或零表示,這樣,就導致了算術根的概念。
算術根的基本性質
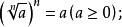 算術根
算術根(1)
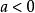 算術根
算術根左方的運算順序代表先求算術根,後乘方,對等式是不一定成立的,例如
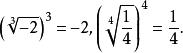 算術根
算術根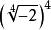 算術根
算術根但是無意義的,當然與-2談不到相等。
它的證明由算術根的定義立即可以得到。
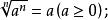 算術根
算術根(2)
左方的運算順序是先乘方,然後求算術根。例如,
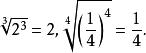 算術根
算術根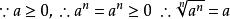 算術根
算術根證明:(依算術根的定義)
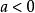 算術根
算術根注意: 時,等式不一定成立。例如
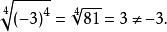 算術根
算術根