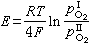激波關係式

激波關係式是一組聯繫激波前後介質運動速度、壓強、溫度、密度等參量的關係式。

激波關係式

正文

一組聯繫激波前後介質運動速度、壓強、溫度、密度等參量的關係式。
在隨激波一起運動的坐標系內，激波是固定不動的。在圖1中激波上的P點，聯繫激波前後介質速度v、壓強p、密度ρ和比焓h(單位質量物質的焓)的質量守恆、動量守恆和能量守恆方程分別為：

下標1、2分別表示激波前後的參量,n、t分別表示沿P點處激波法線方向n和切線方向t的分量。這些基本關係對任何介質，包括氣體、液體和固體都適用，但隨介質的不同可有不同的表達形式（見固體中的激波）。這些關係式通常稱為蘭金－許貢紐關係式。為使上述方程組封閉，還應該補充介質的狀態方程。氣體狀態方程研究得比較充分，固體和液體在高溫、高壓下的狀態方程還需要進一步研究。

對於比熱為常值的完全氣體，利用相應的狀態方程，可以直接解出斜激波後諸氣流參量的關係式：

，

，

式中c＊為臨界聲速(對應於＝1時的聲速)；1為波前氣流的馬赫數；β 為激波相對於波前氣流方向的傾斜角(圖1)；T、s和p0分別為熱力學溫度、比熵(單位質量物質的熵)和總壓；γ 為比熱比。當β 等於90°時，這些關係式就成了正激波關係式。

在正激波中， 存在關係v1v2=c＊2或λ1λ2=1，式中λ＝v/c＊稱為速度係數,在流速等於聲速時，λ＝1。這個關係說明超聲速流（λ1＞1） 經過正激波變為亞聲速流(λ＜1)，相反的變化則是不可能的。從經正激波的熵增(ΔS＝S2-S1)同波前馬赫數的關係（圖2）看出，若波前為亞聲速流(1＜1),則ΔS＜0,這違反熱力學第二定律，故是不可能的。

由質量守恆關係式可直接求出氣流經激波後的折角δ同激波傾斜角β的關係：

。

對於定比熱的完全氣體，這個關係化為：

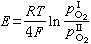
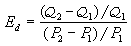
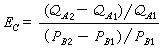
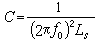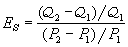
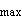對應於一定的1，存在一個最大的折角δ。在馬赫數為1的氣流遇到一半頂角為α 的尖楔時(圖3)，若α＜δ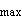，就形成一道依附於尖楔頂端的斜激波；若 α＞δ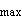則產生一道立在尖楔前方的離體弓形激波。

配圖

相關連線