簡介
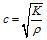 聲速
聲速從本質上講,聲速是介質中微弱壓強擾動的傳播速度,計算公式為:
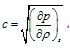 聲速
聲速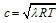 聲速
聲速式中T為熱力學溫度;R為普適氣體常數。對於空氣,,R=287.14焦耳(千克·開),故米/秒。
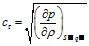 聲速
聲速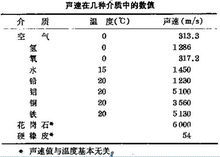 聲速
聲速
音速(velocity of sound,sonic speed)也叫聲速,聲速是介質中微弱壓強擾動的傳播速度,其大小因媒質的性質和狀態而異。空氣中的音速在1個標準大氣壓和15℃的條件下約為340米/秒。在流動的氣體中,相對於氣流而言,微弱擾動的傳播速度也是聲速。在溫度T不為常數的流場中,各點的聲速是不一樣的,與某一點的溫度相當的聲速稱為該點的“當地聲速”。
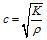 聲速
聲速從本質上講,聲速是介質中微弱壓強擾動的傳播速度,計算公式為:
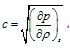 聲速
聲速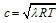 聲速
聲速式中T為熱力學溫度;R為普適氣體常數。對於空氣,,R=287.14焦耳(千克·開),故米/秒。
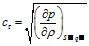 聲速
聲速 聲速
聲速高超聲速技術是指飛行速度超過5倍音速(5馬赫數以上)的飛行器技術,是21世紀航空航天技術的制高點,也是重要的軍民兩用高技術。一個國家要擁有高超聲速的飛行...
簡介 背景 研發 優勢 分類高超聲速飛行器是指飛行速度超過5倍音速的飛機、飛彈、炮彈之類的有翼或無翼飛行器,具有突防成功率高的特點,有著巨大的軍事價值和潛在的經濟價值。
技術難點 發展現狀 各國特點聲速儀是測量海水中聲波傳播速度的儀器,又稱聲速計。現代聲速儀多採用環鳴法(即脈衝循環法)原理。
聲速儀 正文 配圖 相關連線跨聲速流動是流體在流場中速度接近聲速的流動。跨聲速流動可分為外部繞流(如繞翼型、機身等的流動)和內部流動(如噴管、葉柵等處的流動)兩個方面。
跨聲速流動 正文 配圖 相關連線鐵錘高超聲速飛行器是由俄羅斯閃電科學生產聯合體所研製的,這種飛行器器將能攜帶重達800千克的衛星進入200~500千米高的軌道。
簡介 命名由來 研發計畫 套用範圍 相關介紹聲速相對論是流傳極廣的一種對相對論的誤解(科學家已經用實驗驗證了它和它的推論的錯誤),它使人們錯誤的認為,相對論實質上與經典力學是等價的。
聲速相對論 反對聲速相對論的觀點: 科學普及11?3?2 13?4?2 15?3?2
圖書信息 內容簡介 前言 目錄高超聲速流動:所屬現代詞,指的是流體的流動速度遠大於聲速的流動。
高超聲速流動 配圖 相關連線