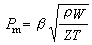激波數值處理
正文
目前有兩種處理方法:一種是激波裝配法,又稱分離奇性法;另一種是激波捕捉法,又稱人工粘性法或穿行法。激波裝配法 這種方法把激波當作未知的運動邊界,按照激波間斷條件把激波分離出來。激波兩邊的物理量要滿足一定的間斷條件,即許貢紐條件(見激波關係式):
D(ρ1-ρ0)=ρ1u1-ρ0u0,(1)
(p1-p0)(ρ1-ρ0)=ρ0(ρ1u1-ρ0u0), (2)
, (3)
tg3β+Atg2β+Btgβ+C=0,(4)
式中A、B、C為U∞和θ的函式, 這個方程不易直接求解,必須用逐步試解法在計算機上求得各種 U∞和θ條件下的β值。在某些情況下,激波是曲面,這時激波位置必須逐點確定。例如,尖頭迴轉體繞流問題(圖2),尖端處產生斜激波OI0。在OA0F0區域流場已知的情況下,可以用特徵線法來求解內部流場B1、C1、D1等點的參量,而激波上的點G0的速度和方向,由下列兩個條件來確定:①滿足激波間斷條件;②滿足F1G0特徵線上相容關係。兩個條件的關係式包含兩個未知數,可以確定 G0的參量。同樣可以確定H0、I0等點的參量,最後把激波和流場計算出來。
在實際流動中,流場中的激波是十分複雜的,用激波裝配法來處理也很困難。一般須用坐標變換,使(尚屬未知的)激波位置與其中的一個坐標軸相重合。美國的G.莫雷蒂和他的同事們就曾用這種方法計算二維超聲速流場中的內伏激波和交叉激波等。
激波裝配法具有精度高,激波位置精確,物理圖像清晰等優點,但計算十分繁複,因此,它只適用於那些激波運動情況比較簡單,圖案可以預估的流動。
激波捕捉法 這是一種在激波層內用直接或間接加入“人工粘性效應”的方法來自動處理激波的近似方法。如果在有激波的流場中人為地加入粘性效應,由於激波所造成的間斷就會變成物理量連續的過渡區,而且只要粘性效應選擇適當,就可以使過渡區具有與計算步長同一量級的寬度。在這個過渡區內,物理量雖然變化很快,卻是光滑過渡的。圖3就是說明由於人工粘性效應使原來不連續的激波(用虛線表示的部分)變成光滑過渡的激波。圖中x為坐標,p0和p1分別表示激波前後的壓力值,由於人工粘性只是在激波附近起主導作用,因此,流場的其他區域仍能保持原來的流動特性。如果用含有人工粘性效應的差分格式來計算,不管激波的位置和強度如何,都可以自動顯示出來。 1950年J.von諾伊曼和R. D.里希特邁爾首先成功地用激波捕捉法處理一維流動中激波。計算中採用
(5)
的人工粘性形成,v為比容,b為經驗係數。從式(5)中可以看出,在稀疏區內q=0;在激波層內,q很大,起光滑作用;在其他壓縮區內q厵0,但很小。過渡區的寬度可根據經驗由係數b來調節,當b取1.5~2時,過渡區一般可控制在 3~5個計算步長。把q項引入運動方程組,可得: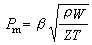 (6)
(6)
(7)
(8)
式中t為時間;x為拉格朗日坐標。用合適的差分格式計算這一方程組,可得到滿意的結果。引入人工粘性要滿足以下條件:①須使激波間斷變成光滑的過渡區,運動方程有連續解;②過渡區寬度應和計算步長同一量級,而且同激波強度、介質狀態無關;③人工粘性只能在激波層內起作用,在激波層外應不影響流場基本特性;④過渡區兩側的物理量仍應滿足激波間斷條件。
除直接引入人工粘性外,還可以通過差分格式間接引入粘性效應,這種粘性稱為格式粘性。把差分方程的各項對某點作泰勒級數展開就可看出,除原微分方程各項外,還增加了一些含計算步長的項。這些低階小量項,主要是一些二階導數項,稱為格式粘性項,它們起光滑作用。以線性雙曲型方程 為例,其拉克斯格式為: 將這差分方程中的各項分別對t和x作泰勒展開並保留二階項,就得到:
,
式中就是格式粘性項,而。在二維流體力學問題中,粘性項必須包括壓縮應力部分和剪應力部分。上述人工粘性項只相當於壓縮應力部分。為了適應二維流體複雜性,可採用既有相當於壓縮應力部分的標量形式的人工粘性項,又有相當於剪應力部分的張量形式人工粘性項。這種張量形式的人工粘性項,不僅可以緩和衝擊壓力的間斷現象,而且對剪下產生的扭曲現象也可起緩衝作用。多維流體力學計算中如何選取人工粘性問題,仍然有待深入研究。
和激波裝配法相比,激波捕捉法比較簡單,但計算精度較差。因此,應該各取兩種方法的長處,例如用裝配法來處理流場外圍的弓形激波,而用捕捉法處理流場內部的複雜激波。
參考書目
R.D.里奇特邁爾著,何旭初等譯:《初值問題差分方法》,科學出版社,北京,1966。(R.D.Richtmyer,Difference Methods for Initialvalue Problems,Interscience Pub., New York,1957.)