特點
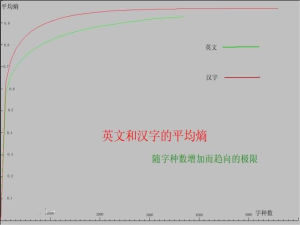 熵
熵1.熵是體系的狀態函式,其值與達到狀態的過程無關;
2.熵的定義式是:dS=dQ/T,因此計算某一過程的熵變時,必須用與這個過程的始態和終態相同的過程的熱效應dQ來計算。(註:如果這裡dQ寫為dQR則表示可逆過程熱效應,R為reversible;dQ寫為dQI為不可逆過程的熱效應,I為Irreversible。)
3.TdS的量綱是能量,而T是強度性質,因此S是廣度性質。計算時,必須考慮體系的質量;
4.同狀態函式U和H一樣,一般只計算熵的變化。
歷史
概念提出
1850年,德國物理學家魯道夫·克勞修斯首次提出熵的概念,用來表示任何一種能量在空間中分布的混亂程度,能量分布得越混亂,熵就越大。一個體系的能量完全均勻分布時,這個系統的熵就達到最大值。在克勞修斯看來,在一個系統中,如果聽任它自然發展,那么,能量差總是傾向於消除的。讓一個熱物體同一個冷物體相接觸,熱就會以下面所說的方式流動:熱物體將冷卻,冷物體將變熱,直到兩個物體達到相同的溫度為止。克勞修斯在研究卡諾熱機時,根據卡諾定理得出了對任意可逆循環過程都適用的一個公式:dS=dQ/T。
證明
對於絕熱過程Q=0,故S≥0,(因為Q無變化,系統處於無限趨於平衡狀態,熵會無限增大,因為平衡狀態是理想狀態,永遠達不到,為dS>0。)即系統的熵在可逆絕熱過程中不變,在不可逆絕熱過程中單調增大。這就是熵增加原理。由於孤立系統內部的一切變化與外界無關,必然是絕熱過程,所以熵增加原理也可表為:一個孤立系統的熵永遠不會減少。它表明隨著孤立系統由非平衡態趨於平衡態,其熵單調增大,當系統達到平衡態時,熵達到最大值。熵的變化和最大值確定了孤立系統過程進行的方向和限度,熵增加原理就是熱力學第二定律。
1948年,克勞德·艾爾伍德·香農(ClaudeElwoodShannon)在BellSystemTechnicalJournal上發表了《通信的數學原理》(AMathematicalTheoryofCommunication)一文,將熵的概念引入資訊理論中。
函式來歷
熱力學第一定律就是能量守恆與轉換定律,但是它並未涉及能量轉換的過程能否自發地進行以及可進行到何種程度。熱力學第二定律就是判斷自發過程進行的方向和限度的定律,它有不同的表述方法。
克勞修斯的描述①熱量不可能自發地從低溫物體傳到高溫物體,即熱量不可能從低溫物體傳到高溫物體而不引起其他變化;
開爾文的描述②不可能從單一熱源取出熱量使之全部轉化為功而不發生其他影響;
因此第二類永動機是不可能造成的。熱力學第二定律是人類經驗的總結,它不能從其他更普遍的定律推導出來,但是迄今為止沒有一個實驗事實與之相違背,它是基本的自然法則之一。
由於一切熱力學變化(包括相變化和化學變化)的方向和限度都可歸結為熱和功之間的相互轉化及其轉化限度的問題,那么就一定能找到一個普遍的熱力學函式來判別自發過程的方向和限度。可以構想,這種函式是一種狀態函式,又是一個判別性函式(有符號差異),它能定量說明自發過程的趨勢大小,這種狀態函式就是熵函式。
如果把任意的可逆循環分割成許多小的卡諾循環,可得出∑(δQi/Ti)r=0(1)即任意的可逆循環過程的熱溫熵之和為零。其中,δQi為任意無限小可逆循環中系統與環境的熱交換量;Ti為任意無限小可逆循環中系統的溫度。上式也可寫成∮(δQr/T)=0(2)克勞修斯總結了這一規律,稱這個狀態函式為“熵”,用S來表示,即dS=δQr/T(3)對於不可逆過程,則可得dS>δQr/T(4)或dS-δQr/T>0(5)這就是克勞修斯不等式,表明了一個隔離系統在經歷了一個微小不可逆變化後,系統的熵變大於過程中的熱溫熵。對於任一過程(包括可逆與不可逆過程),則有dS-δQ/T≥0(6)式中:不等號適用於不可逆過程,等號適用於可逆過程。由於不可逆過程是所有自發過程之共同特徵,而可逆過程的每一步微小變化,都無限接近於平衡狀態,因此這一平衡狀態正是不可逆過程所能達到的限度。因此,上式也可作為判斷這一過程自發與否的判據,稱為“熵判據”。對於絕熱過程,δQ=0,代入上式,則dSj≥0(7)。由此可見,在絕熱過程中,系統的熵值永不減少。其中,對於可逆的絕熱過程,dSj=0,即系統的熵值不變;對於不可逆的絕熱過程,dSj>0,即系統的熵值增加。這就是“熵增原理”,是熱力學第二定律的數學表述,即在隔離或絕熱條件下,系統進行自發過程的方向總是熵值增大的方向,直到熵值達到最大值,此時系統達到平衡狀態。
意義
統計學
玻爾茲曼在研究分子運動統計現象的基礎上提出了公式:S=k×lnΩ(8)其中,Ω為系統分子的狀態數,k為玻爾茲曼常數。這個公式反映了熵函式的統計學意義,它將系統的巨觀物理量S與微觀物理量Ω聯繫起來,成為聯繫巨觀與微觀的重要橋樑之一。基於上述熵與熱力學幾率之間的關係,可以得出結論:系統的熵值直接反映了它所處狀態的均勻程度,系統的熵值越小,它所處的狀態越是有序,越不均勻;系統的熵值越大,它所處的狀態越是無序,越均勻。系統總是力圖自發地從熵值較小的狀態向熵值較大(即從有序走向無序)的狀態轉變,這就是隔離系統“熵值增大原理”的微觀物理意義。
物理學
 熵
熵決定反應方向主要有兩個因素:
(1)反應熱效應。放熱反應使體系的能量下降
(2)混亂度。一些吸熱反應在一定溫度下也可進行特點是反應體系的混亂度變大。體系的微觀狀態數越多,體系的混亂度越大,微觀狀態數可以定量地表明體系的混亂度。
2、狀態函式
熵:描述體系混亂度的狀態函式叫做熵,用S表示。體系的狀態一定,其微觀狀態數一定,如果用狀態函式來表示混亂度的話,狀態函式與微觀狀態數Ω存在下列關係S=klnΩ,其中k=1.38×10-23J/K叫波爾茲曼常數。熵是一種具有加和性的狀態函式,體系的熵值越大則微觀狀態數Ω的越大,即混亂度越大,因此可以認為化學反應趨向於熵值增加,即趨向於∆rS>0。過程的始終態一定,狀態函式S的改變數∆S的值是一定的,過程中的熱量變化是和途徑有關的量,若以可逆方式完成這一過程時,熱量用Qr表示,則∆S=Qr/T。在373K,1.013×105Pa時HO(l)→HO(g)的相變熱為44.0kJ/mol故此過程的摩爾熵變∆Sm=Qr/T=44.0×103/373=118(J/mol·K)
3、熱力學第三定律和標準熵
熱力學第三定律:在0K時任何完整晶體中的原子或分子只有一種排列方式,即只有唯一的微觀狀態,其熵值為零。從熵值為零的狀態出發,使體系變化到P=1.013×105Pa和某溫度T,如果知道這一過程中的熱力學數據,原則上可以求出過程的熵變值,它就是體系的絕對熵值。於是人們求得了各種物質在標準狀態下的摩爾絕對熵值,簡稱標準熵,單位為kJ/mol。
基本特性
熵均大於等於零,即,H>=0。
·設N是系統S內的事件總數,則熵H<=log2(N)。若且唯若p1=p2=...=pn時,等號成立,此時熵最大。
·聯合熵:H(X,Y)=H(X)+H(Y),若且唯若X,Y在統計學上相互獨立時等號成立。
·條件熵:H(X|Y)=H(X,Y)-H(Y)=H(X),若且唯若X,Y在統計學上相互獨立時等號成立。
·社會學意義:從巨觀上表示世界和社會在進化過程中的混亂程度。
按照一些後現代的西方社會學家觀點,熵的概念被其移植到社會學中。表示隨著人類社會隨著科學技術的發展及文明程度的提高,社會“熵”——即社會生存狀態及社會價值觀的混亂程度將不斷增加。按其學術觀點,現代社會中恐怖主義肆虐,疾病疫病流行,社會革命,經濟危機爆發周期縮短,人性物化都是社會“熵”增加的表征。
如今年多次獲諾貝爾文學獎提名的托馬斯·品欽在大學畢業之後發表在雜誌上的短篇小說《熵》,即闡釋了熵的社會學概念。這篇小說將熱力學的第二定律運用到對人類社會的描述上,其敏感性令人大吃一驚。所謂的熱力學第二定律,指的就是孤立系統熵恆定的定律。熵指的是物質系統的熱力學函式,在整個宇宙當中,當一種物質轉化成另外一種物質之後,不僅不可逆轉物質形態,而且會有越來越多的能量變得不可利用。也就是說,大量人類製造的化工產品、能源產品一經使用,不可能再變成有利的東西,宇宙本身在物質的增殖中走向“熱寂”,走向一種緩慢的熵值不斷增加的死亡。眼下人類社會正是這個樣子:大量的產品和能源轉化成不能逆轉的東西,垃圾越來越多,人類社會逐步地走向一個惡化的熱寂死亡狀態。托馬斯·品欽後來主要的小說多次地、不斷地闡釋著這個熵的世界觀。
根據“熱力學第二定律”,作為一個“孤立”的系統,宇宙的“熵”會隨著時間的流逝而增加,由有序向無序,當宇宙的“熵”達到最大值時,宇宙中的其他有效能量已經全數轉化為無效能量,所有物質溫度達到熱平衡。這樣的宇宙中再也沒有任何可以維持運動或是生命的能量存在。當熱寂達到絕對零度時所有分子都已停止運動。
套用
熱力學
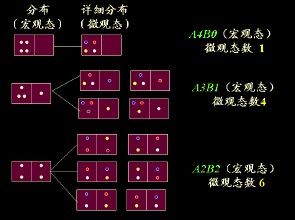 熵
熵單位質量物質的熵稱為比熵,記為s。熵最初是根據熱力學第二定律引出的一個反映自發過程不可逆性的物質狀態參量。
熱力學第二定律是根據大量觀察結果總結出來的規律,有下述表述方式:
①熱量總是從高溫物體傳到低溫物體,不可能作相反的傳遞而不引起其他的變化;
②功可以全部轉化為熱,但任何熱機不能全部地、連續不斷地把所接受的熱量轉變為功,而不產生其他任何影響(即無法製造第二類永動機);
③在孤立系統中,實際發生的過程總使整個系統的熵值增大,此即熵增原理。摩擦使一部分機械能不可逆地轉變為熱,使熵增加。
熱量dQ由高溫(T1)物體傳至低溫(T2)物體高溫物體的熵減少dS1=dQ/T1,低溫物體的熵增加dS2=dQ/T2,把兩個物體合起來當成一個系統來看,熵的變化是dS=dS2+dS1>0,即熵是增加的。
物理學家玻爾茲曼將熵定義為一種特殊狀態的機率:原子聚集方式的數量。可精確表示為:S=K㏑WK是比例常數,稱為玻爾茲曼常數。
科學哲學
科學技術上泛指某些物質系統狀態的一種量(liàng)度,某些物質系統狀態可能出現的程度。亦被社會科學用以借喻人類社會某些狀態的程度。熵是不能再被轉化做功的能量的總和的測定單位。這個名稱是由熱力學奠基人之一,德國物理學家魯道爾夫·克勞修斯(1822—1888)於1868年第一次提出來的。但是年輕的法國軍官、物理學家、工程師沙迪·迦諾(1796—1832)一般譯作“卡諾”,在研究熱機效率的過程中,提出了“卡諾循環”定理,卻比克勞修斯早41年發現了熵的原理。迦諾在研究蒸汽機工作原理時發現,蒸汽機之所以能做功,是因為蒸汽機系統里的一部分很冷,而另一部分卻很熱。換一句話說,要把能量轉化為功,一個系統的不同部分之間就必須有能量集中程度的差異。當能量從一個較高的集中程度轉化到一個較低的集中程度時,它就做了功。更重要的是每一次能量從一個水平轉化到另一個水平,都意味著下一次能再做功的能量就減少了。比如河水越過水壩流入湖泊。當河水下落時,它可被用來發電,驅動水輪,或做其他形式的功。然而水一旦落到壩底,就處於不能再做功的狀態了。在水平面上沒有任何勢能的水是連最小的輪子也帶不動的。這兩種不同的能量狀態分別被稱為“有效的”或“自由的”能量,和“無效的”或“封閉的”能量。
熵的增加就意味著有效能量的減少。每當自然界發生任何事情,一定的能量就被轉化成了不能再做功的無效能量。被轉化成了無效狀態的能量構成了我們所說的污染。許多人以為污染是生產的副產品,但實際上它只是世界上轉化成無效能量的全部有效能量的總和。耗散了的能量就是污染。既然根據熱力學第一定律,能量既不能被產生又不能被消滅,而根據熱力學第二定律,能量只能沿著一個方向——即耗散的方向——轉化,那么污染就是熵的同義詞。它是某一系統中存在的一定單位的無效能量。
生命科學
生命體是一個開放的系統,時刻與外界進行著物質、能量、信息的交換,符合“耗散結構”,可以用熵來分析一個生命體從生長、衰老、病死的全過程,用“生命熵”來獨立定義。
生命熵的內容包含生命現象的時間序、空間結構序與功能序,生命熵變就直接反應這三個序的程度變化之和。
詞源
熵(entropy)這一中文譯名是意譯而來的。“entropy”最初由克勞修斯(Clausius)於1865年創造的。字尾“tropy”源於希臘文“trop-”,“turn”or“change”是轉變之意。“en-”是來自希臘語的前綴,意思是“within”。entropy便是“changewithin(aclosedsystem)”。1923年,德國物理學家普朗克(I.R.Planck)來南京第四中山大學(即中央大學前身)講學,我國著名物理學家胡剛復教授(時任南京第四中山大學自然科學院院長)擔任翻譯。胡剛復教授根據entropy意為熱量與溫度之商,而且這個概念與火有關,就在商上另加火旁,首次創造了中國字典中從未有過的新字“熵”。此字含義極其妥帖,沿用至今。
概念出處
在19世紀60年代,有人曾十分戲劇性地描繪了“世界末日”的情景:“宇宙越是接近於其熵為一最大值的極限狀態,它繼續發生變化的可能就越小;當它完全達到這個狀態時,就不會再出現進一步的變化了,宇宙將永遠處於一種惰性的死寂狀態。”這就是轟動一時的“宇宙熱寂論”。德國科學家克勞修斯,他提出的“熵”的概念和熱力學第二定律。
大學教授
魯道夫.克勞修斯(RudolfJuliusEmanuelClausisu)是德國物理學家、熱力學奠基人之一。1822年1月2日,克勞修斯出生於波蘭科沙林。父親是國小校長。克勞修斯就是在他父親創辦的學校里接受了人生的啟蒙教育。在國小里,克勞修斯是個聰明調皮的學生,尤其在數理方面有著與眾不同的才能,而他父親也就有意識地培育他這方面的興趣和能力。國小畢業後,克勞修斯進入斯德丁中學繼續他的學業,隨後於1840年順利考入柏林大學。在大學裡,克勞修斯如魚得水,學習非常努力,而且興趣廣泛。他一度對歷史產生了濃厚的興趣,準備從事歷史研究,但又始終放不下對數理科學的鐘愛。克勞修斯的父母和老師都積極支持克勞修斯在數理方面發展,認為他有這方面的天賦,克勞修斯自己也覺得真正喜歡的還是數理科學,因此,他最後還是決定選擇數理研究作為自己的專攻方向。在柏林大學完成了大學學業以後,克勞修斯又進入哈雷大學,攻讀主修數學和物理的哲學博士學位。1847年,克勞修斯獲得博士學位,開始在柏林炮兵工程學院任教,擔任物理課教師。
1850年,克勞修斯發表了一篇關於熱的理論的論文,這是他第一次發表比較有份量的科研文章,但立刻引起了科學界的關注。在文中他提出的觀點,後來被認為是熱力學的第二定律。柏林炮兵工程學院對這位年輕的小伙子青睞有加,不久便破格聘他擔任學校的教授職位,如此年輕便擔任教授一職,這在學院還是第一次。但是克勞修斯在炮兵工程學院的任職時間並不長。1859年,他來到蘇黎世工業大學,擔任物理學教授。蘇黎世工業大學給克勞修斯的研究提供了良好的環境。在這裡,他全身心地投入到物理學的研究之中。克勞修斯研究的視野非常開闊,成就非凡,尤其在熱力學方面,經過近10年的研究,他得出了熱力學的“克勞修斯不等式”,隨即提出了“熵”這一熱力學上的重要概念。克勞修斯在蘇黎世工業大學前後一共工作了12年,這期間他在科學研究上碩果纍纍,成為世人公認的大科學家。1869年克勞修斯返回德國,擔任維爾茨堡大學教授,兩年後,他又移居波恩,擔任波恩大學教授,繼續從事他的物理科學研究。克勞修斯在波恩大學的研究工作並不順利,條件也比較艱苦。1870~1871年普法戰爭全面爆發。克勞修斯帶領一個學生救護小組,四處救助傷員,不幸卻嚴重損壞了自己的膝蓋,從此長期受到傷痛的折磨,不得不將學生的實驗課交給其他老師負責。此後不久,克勞修斯又遭到更為沉重的打擊,他的妻子在生第6個孩子時去世,這不但在精神上使克勞修斯備感蒼涼,而且從此他不得不把一部分精力從科學研究中分出來,獨立承擔起照顧家庭的重任。儘管如此,克勞修斯還是在研究中取得了許多新的成就。1888年8月24日,克勞修斯工作到最後一刻黯然去世。
奠基者
克勞修斯一生研究廣泛,但最著名的成就是提出了熱力學第二定律,成為熱力學理論的奠基人之一。
人類科學發展到19世紀,蒸汽機的套用已經十分廣泛,如何進一步提高熱機的效率問題越來越受到人們的重視,成了理論物理研究的重點課題。1824年,卡諾在熱質說和永動機不可能的基礎上證明了後來著名的卡諾定理,這不僅推論出了熱機效率的最上限,而且也包含了熱力學第二定律的若干內容。此後,經過許多科學家長期的研究,到19世紀中葉,能量轉化和守恆定律建立了起來,這個物理學中極其重要的普遍規律,很快就成為研究熱和其他各種運動形式相互轉化的堅實基礎。
克勞修斯從青年時代起,就決定對熱力進行理論上的研究,他認為一旦在理論上有了突破,那么提高熱機的效率問題就可以迎刃而解。有了明確目標,克勞修斯學習異常勤奮,他知道只有在學生階段打下堅實的數理基礎,才能在今後的研究道路上有所建樹。因此,克勞修斯用了近10年時間在學校里埋頭苦讀。有志者事竟成,1850年,克勞修斯發表了第一篇關於熱的理論的論文——《論熱的動力以及由此推出關於熱本身的定律》。在論文裡,他首先以當時焦耳用實驗方法所確立的熱功當量為基礎,第一次明確提出了熱力學第一定律:在一切由熱產生功的情況中,必有和所產生的功成正比的熱量被消耗掉;反之,消耗同樣數量的功,也就會產生同樣數量的熱。按照這個基本定律,克勞修斯又以理想氣體為例,進行進一步的論述,否定了熱質理論的基本前提,即宇宙中的熱量守恆,物質內部的熱量是物質狀態函式的觀點。
在熱力學第一定律的基礎上,克勞修斯接著在論文的第二部分,重新論證了卡諾於1824年得出的“卡諾定律”——工作於兩個溫度間的一切理想熱機,有同樣多的熱量轉移而得到同樣多的功,且與工作物質無關,在這個循環過程中熱量並未消失。克勞修斯經過精密的論證後認為,卡諾定理的基本內容是正確的,但熱量的沒有消失顯然和熱功當量相矛盾,因此卡諾在論證過程中所依託的“熱質守恆”是不可信的。克勞修斯指出,根據我們的日常經驗,要使熱從低溫物體傳向高溫物體,必須要消耗某種動力或者有其他的一些變化。在沒有任何形式變化的情況下,熱必定是從高溫物體向低溫物體轉移。這一著名的論斷就是熱力學第二定律的基本內容。
熱力學第一、第二定律的確立,標誌著熱力學基本理論的完成。克勞修斯因提出熱力學第二定律而聲譽雀起,年紀輕輕就躋身於科學家的行列。但科學道路永無止境,克勞修斯一如既往地在科學道路上長途跋涉。
概念的提出
為了進一步推動熱的動力學說,克勞修斯把理論和實驗結合起來,進行深入的研究。在研究卡諾熱機操作循環過程中,他發現熱量在減少的同時,卻可以看出有一個量在整個循環的過程中自始至終保持不變。如果是在理想過程中的話,那么這個比值是個常數,而且從不會減少。這也就是說,在密閉系統中,系統的熱量和系統的絕對溫度的比值在任何過程中都是增長的。這個不小的發現使克勞修斯驚喜不已,他隱約感覺到自己的研究又將出現新的突破。於是,他不斷地實驗,反覆地論證,把所有的精力都傾注在這個“恆量”的研究之中。1854年,克勞修斯把研究的結果以論文的形式予以發表,在文中,他提出了著名的“克勞修斯不等式”,得出了卡諾熱機效率的公式,並推廣到任何一個可逆的循環之中。1865年,克勞修斯發表了《力學的熱理論的主要方程之便於套用的形式》一文,在文中明確表達了“熵”的概念。熵是物質的狀態函式,即狀態一定時,物質的熵值也一定。從分子運動論的觀點來看,由於分子的熱運動,物質系統的分子要從有序趨向無序,熵變大則表示分子運動無序程度的增加。克勞修斯用大量的理論和事實依據嚴格證明,一個孤立的系統的熵永遠不會減少,此即熵增加原理。
有了熵的概念,熱力學第二定律可以從數學上表述為熵增加原理,他揭示了自然界中這樣的一個事實:在一個可逆的過程中,系統的熵越大,就越接近平衡狀態,雖然此間能量的數量不變,但可供利用或者是轉化的能量卻是越來越少。克勞修斯用熵的概念來定量地表述熱力學的第二定律,為熱力學的發展開闢了全新的道路,人們通過這一簡潔的定理,對熱運動學說有了更為全面的認識。就這樣,熱力學第一定律闡明了熱在轉化過程中各種能量總是保持不變的規律,熵增加原理則定量地揭示出巨觀過程的方向性和限度,兩個定律相互交織,構成了一幅完整的圖畫,使人們對熱現象的能量轉化過程的基本特徵有了全面的認識。
在1865年的論文末尾,克勞修斯把熱力學第一、第二定律擴大到適用於整個宇宙範圍,他認為宇宙的能量是個常數,宇宙的熵趨於某一最大值。此後,他在一次講演中進一步指出:宇宙的熵越接近某一最大的極限值,那么它變化的可能性越小,宇宙將永遠處於一種惰性的死寂狀態。這就是所謂的“熱寂說”。克勞修斯這個觀點顯然是錯誤的。恩格斯在這種理論剛出現不久,就對它進行了批判,指出導致熱寂說錯誤的一個重要原因是克勞修斯贊同“能消失了,如果不是在量上,那也是在質上消失了”。現代自然科學證明,宇宙中熱循環的形式是多種多樣的,各種運動形式都可以互相轉化,宇宙間熵的增加和減少的系統都是存在的。
貢獻
作為熱力學理論的奠基人,克勞修斯一生的成就遠不止於此,他在許多方面都取得了令人矚目的研究成果,尤其在氣體分子運動論方面,人們也習慣性地把他和麥克斯韋、玻爾茲曼一起稱為分子運動論的奠基人。
早在18世紀,科學家們就發現氣體是由大量激烈運動的粒子組成的,氣體的壓力來自於粒子對器壁的碰撞。到了19世紀50年代,克勞修斯等建立了熱力學理論,並用熱的運動學說作為基礎來進行分子運動研究,這大大促進了分子運動學說的發展。1857年,克勞修斯發表了一篇具有奠基性質的論文《論我們稱之為熱的那種運動》,論文內容豐富,闡述了多個有關分子運動的問題。克勞修斯從氣體是運動分子集合體的觀點出發,認為考察單個分子的運動既不可能也毫無意義,系統的巨觀性質不是取決於一個或某些分子的運動,而是取決於大量分子運動的平均值。因此,他提出了統計平均的概念,這是建立分子運動論的前提。根據這個前提,克勞修斯建立了理想氣體分子運動的模型,並強調分子的動能不僅是它們的直線運動,而且是分子中原子鏇轉和振盪的運動,從而正確地確定了實際氣體和理想氣體的區別。在此基礎上,克勞修斯計算了碰撞器壁的分子數和相應的分子的動量變化,並通過一系列複雜的演算和論證,最終得出了因分子碰撞而施加給器壁的壓強公式,從而揭示了氣體定律的微觀本質。不僅如此,克勞修斯還把目光投向了氣體的固態和液態。他論斷說:三種聚集態中的分子都在運動,只是運動的方式有所差異而已。
在1857年的論文中,克勞修斯第一次計算得到了氧、氮、氫3種氣體分子在冰點時的速率。然而這個氣體分子運動速度高達每秒數百米的結論,遠遠超出了人們的意料,因為在現實生活中,氣體的擴散(比如煙霧的瀰漫)過程是相當的緩慢,因此人們對於克勞修斯的研究成果表示了極大的懷疑。如何才能解釋這個根據理論計算得出的分子運動速度,與氣體擴散現象所顯示的速度二者之間的矛盾呢?克勞修斯陷入了新的困惑之中。他意識到,自己以前把分子看作數學上幾何點的模型不夠確切,必須加以修正。他從分析氣體分子間的相互碰撞入手,把分子的作用範圍作為他依據的主要概念,引入了在單位時間內所發生的碰撞數和分子運動的自由程兩個概念,並得出了第一個平均自由程的公式。通過這些全新的研究方法,克勞修斯認為,儘管單個分子運動的速度非常快,但由於分子間的相互碰撞,分子運動的軌跡十分曲折,就整個分子的集合體而言,其前進的路程就更加漫長,遠遠小於分子運動速度給出的結果,這也就是氣體擴散緩慢的原因。克勞修斯開創性地解決了氣體擴散速度小於分子運動速度之間的矛盾,終於打消了人們心頭的疑慮,使得他們對於分子運動論充滿了信心,開闢了研究氣體運動現象的道路。
![熵[物理學術語] 熵[物理學術語]](/img/0/5b4/nBnauM3X3YDNzcTMzUDM0YzM2QTM5QDO1gzNzQTNwAzMwIzL1AzLxczLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg)
