定理
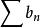 比較審斂法
比較審斂法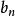 比較審斂法
比較審斂法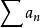 比較審斂法
比較審斂法 比較審斂法
比較審斂法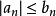 比較審斂法
比較審斂法設 為一收斂的無窮級數,當中每項 都是正實數,而無窮級數 中的 可為複數。假定對任意n有 (這裡代表取複數的模)。
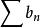 比較審斂法
比較審斂法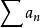 比較審斂法
比較審斂法(1)若 收斂,則 收斂。
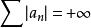 比較審斂法
比較審斂法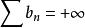 比較審斂法
比較審斂法(2)若 ,則級數 。
證明
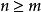 比較審斂法
比較審斂法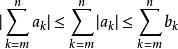 比較審斂法
比較審斂法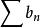 比較審斂法
比較審斂法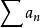 比較審斂法
比較審斂法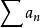 比較審斂法
比較審斂法(1)對於 有 ,第一個不等號是因有三角不等式而成立。按假定, 符合柯西收斂原理,所以 亦然。因為複數集的完備性,知 收斂。
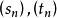 比較審斂法
比較審斂法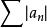 比較審斂法
比較審斂法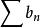 比較審斂法
比較審斂法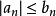 比較審斂法
比較審斂法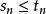 比較審斂法
比較審斂法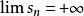 比較審斂法
比較審斂法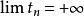 比較審斂法
比較審斂法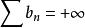 比較審斂法
比較審斂法(2)設數列 分別代表 , 的部分和。因為對任意n有 ,所以 。由於 ,根據極限的保不等式性, ,即 。
推論
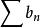 比較審斂法
比較審斂法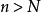 比較審斂法
比較審斂法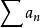 比較審斂法
比較審斂法(1)如果級數 收斂,且存在正整數N,使當 時,(k>0)成立,則級數 收斂;
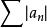 比較審斂法
比較審斂法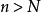 比較審斂法
比較審斂法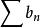 比較審斂法
比較審斂法(2)如果級數 發散,且存在正整數N,使當 時,(k>0)成立,則級數 發散。
典型題
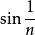 比較審斂法
比較審斂法判斷一般項為 的無窮級數的收斂性:
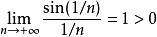 比較審斂法
比較審斂法因為 ,而一般項為1/n的級數發散(調和級數發散),由比較審斂法知此級數發散。

